练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知一个5次多项式为f（x）=3x5﹣2x4+5x3﹣2.5x2+1.5x﹣0.7，用秦九韶算法求出这个多项式当x=4时的值．

    【答案】【解答】解：f（x）=3x5﹣2x4+5x3﹣2.5x2+1.5x﹣0.7=（（（（3x﹣2）x+5）x﹣2.5）x+1.5）x﹣0.7，

    v0=3，v1=3×4﹣2=10，v2=10×4+5=45，v3=45×4﹣2.5=177.5，v4=177.5×4+1.5=711.5，v5=711.5×4﹣0.7=2845.3．


    【解析】f（x）=3x5﹣2x4+5x3﹣2.5x2+1.5x﹣0.7=（（（（3x﹣2）x+5）x﹣2.5）x+1.5）x﹣0.7，,即可求出。
    【考点精析】利用秦九韶算法对题目进行判断即可得到答案，需要熟知求多项式的值时，首先计算最内层括号内依次多项式的值，即v1=anx+an-1然后由内向外逐层计算一次多项式的值，把n次多项式的求值问题转化成求n个一次多项式的值的问题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图线段AB过x轴正半轴上一定点M（m，0），端点A、B到x轴距离之积为2m，以x轴为对称轴，过A，O，B三点作抛物线．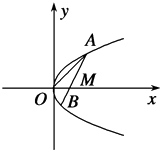
    （1）求抛物线方程；
    （2）若 =﹣1，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（cosx，sinx）， =（3，﹣ ），x∈[0，π]
    （1）若 ∥ ，求x的值；
    （2）记f（x）= ，求f（x）的最大值和最小值以及对应的x的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足an+1=an﹣2anan+1 ， an≠0且a1=1．
    （1）求数列{an}的通项公式；
    （2）令 ，求数列{bn}的前2n项和T2n ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆O： （a＞b＞0）过点（ ，﹣ ），A（x0 ， y0）（x0y0≠0），其上顶点到直线 x+y+3=0的距离为2，过点A的直线l与x，y轴的交点分别为M、N，且 =2 ．
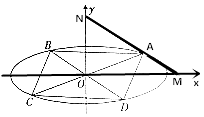
    （1）证明：|MN|为定值；
    （2）如图所示，若A，C关于原点对称，B，D关于原点对称，且 =λ ，求四边形ABCD面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】执行如图所示的程序框图，则输出的a值为（ ）
    A.﹣3
    B.
    C.﹣
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了适应市场需要，某地准备建一个圆形生猪储备基地(如右图)，它的附近有一条公路，从基地中心O处向东走1 km是储备基地的边界上的点A ， 接着向东再走7 km到达公路上的点B；从基地中心O向正北走8 km到达公路的另一点C.现准备在储备基地的边界上选一点D ， 修建一条由D通往公路BC的专用线DE ， 求DE的最短距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】①“x∈R，x2﹣3x+3=0”的否定是真命题； ②“ ”是“2x2﹣5x﹣3＜0”必要不充分条件；
    ③“若xy=0，则x，y中至少有一个为0”的否命题是真命题；
    ④曲线 与曲线 有相同的焦点；
    ⑤过点（1，3）且与抛物线y2=4x相切的直线有且只有一条．
    其中是真命题的有：（把你认为正确命题的序号都填上）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= x2+ax+1（a∈R）． （Ⅰ）当a= 时，求不等式f（x）＜3的解集；
    （Ⅱ）当0＜x＜2时，不等式f（x）＞0恒成立，求实数a的取值范围；
    （Ⅲ）求关于x的不等式f（x）﹣ a2﹣1＞0的解集．

    查看答案和解析>>

    同步练习册答案