
����Ŀ��Ϊ���˽�ס�������������������̥�Ŀ����Ƿ��꣬�ֱ�����������ѡȡ��![]() ����̥����ÿ����̥�Ŀ��ȣ���λ��
����̥����ÿ����̥�Ŀ��ȣ���λ�� ![]() ����¼���������Ƴ����µ�����ͼ��
����¼���������Ƴ����µ�����ͼ��
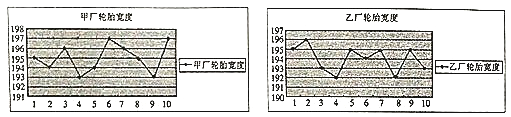
��1���ֱ����ס��������ṩ��![]() ����̥���ȵ�ƽ��ֵ��
����̥���ȵ�ƽ��ֵ��
��2����̥�Ŀ�����![]() �ڣ���������̥�DZ���̥.
�ڣ���������̥�DZ���̥.
��i�����Ӽ����ṩ��![]() ����̥�����ѡȡ
����̥�����ѡȡ![]() ��������ѡ����̥�DZ���̥�ĸ���
��������ѡ����̥�DZ���̥�ĸ���![]() ��
��
��ii���ԱȽϼס��������ֱ��ṩ��![]() ����̥�����б���̥���ȵķ����С�����������ı���̥���ȵ�ƽ��ˮƽ���䲨��������ж������������ĸ�������̥��Ը��ã�
����̥�����б���̥���ȵķ����С�����������ı���̥���ȵ�ƽ��ˮƽ���䲨��������ж������������ĸ�������̥��Ը��ã�
���𰸡���1��![]()
![]() .
.![]()
![]() .��2����i��
.��2����i��![]() .��ii��������.
.��ii��������.
�������������������1����������ͼ������׳�������̥���ȵ�ƽ��ֵ���ҳ�������̥���ȵ�ƽ��ֵ��
��2�����ٴӼ׳��ṩ��10����̥����6����̥�DZ���̥���������ѡȡ1�����������ѡ����̥�DZ���̥�ĸ��ʣ�
�ڼ׳�������̥���ȶ���[194��196]�ڵ�����Ϊ195��194��196��194��196��195���ҳ�������̥���ȶ���[194��196]�ڵ�����Ϊ195��196��195��194��195��195�������������̥���ȵ�ƽ������ȣ����ҳ��ķ����С���Ӷ��ҳ�����̥��Ը��ã�
���������
��1���׳�������̥���ȵ�ƽ��ֵΪ
![]()
![]()
![]() .
.
�ҳ�������̥���ȵ�ƽ��ֵΪ
![]()
![]()
![]() .
.
��2���׳�������̥���ȶ���![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
��i��![]() .
.
��ii���׳�����̥��ƽ����Ϊ![]() ������Ϊ
������Ϊ![]() .
.
�ҳ�������̥���ȶ���![]() �ڵ�����Ϊ
�ڵ�����Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
ƽ����Ϊ![]() ������Ϊ
������Ϊ![]() .
.
������������̥���ȵ�ƽ������ȣ����ҵķ����С�������ҳ�����̥��Ը���.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC�� ![]() =1��a��b��0����������Ϊ
=1��a��b��0����������Ϊ ![]() �����߷�����x=��2����OΪԭ�㣬��A����ԲC�ϣ���B��ֱ��y=2�ϣ���OA��OB��
�����߷�����x=��2����OΪԭ�㣬��A����ԲC�ϣ���B��ֱ��y=2�ϣ���OA��OB�� 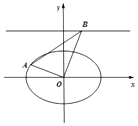
��1������ԲC�ķ��̣�
��2�����AOB���ȡ����Сֵʱ���߶�AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ס�������ѧУȫ������꼶ѧ���ڸõ�����У�����е���ѧ�ɼ����������У�������ȡ60��ѧ������������������Ƶ���ֲ�ͳ�Ʊ����£� ��У��
���� | [70��80�� | [80��90�� | [90��100�� | [100��110�� |
Ƶ�� | 2 | 5 | 9 | 10 |
���� | [110��120�� | [120��130�� | [130��140�� | [140��150] |
Ƶ�� | 14 | 10 | 6 | 4 |
����
���� | [70��80�� | [80��90�� | [90��100�� | [100��110�� |
Ƶ�� | 2 | 4 | 8 | 16 |
���� | [110��120�� | [120��130�� | [130��140�� | [140��150] |
Ƶ�� | 15 | 6 | 6 | 3 |
�Գ��������������ݹ�������
��1���Ƚϼס�����Уѧ������ѧƽ���ɼ��ĸߵͣ�
��2�����涨��ѧ�ɼ�������120��Ϊ���㣬�Ӽס�����Уȫ�����ѧ���и������ȡ2�ˣ�������ѧ�ɼ�Ϊ����Ĺ�X�ˣ���X�ķֲ��м���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȳ�����{an}��ǰn���ΪSn �� ��֪a2=7��a3Ϊ��������Sn�����ֵΪS5 ��
��1����{an}��ͨ�ʽ��
��2����bn= ![]() ��������{bn}��ǰn���Tn ��
��������{bn}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C1�ļ����귽��Ϊ��2cos2��=18������C2�ļ����귽��Ϊ��= ![]() ������C1 �� C2�ཻ��A��B���㣮
������C1 �� C2�ཻ��A��B���㣮
��1����A��B����ļ����ꣻ
��2������C1��ֱ��  ��tΪ�������ֱ��ཻ��M��N���㣬���߶�MN�ij��ȣ�
��tΪ�������ֱ��ཻ��M��N���㣬���߶�MN�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ƻ����˾����ij��iphone�ֻ�����̶��ɱ�Ϊ40����Ԫ��ÿ����1ֻ������Ͷ��16��Ԫ����ƻ����˾һ���ڹ������ÿ�iphone�ֻ�x��ֻ��ȫ�������꣬ÿ��ֻ����������ΪR��x������Ԫ����R��x��= 
��1��д��������W����Ԫ�����������x����ֻ���ĺ�������ʽ��
��2���������Ϊ������ֻʱ��ƻ����˾�ڸÿ��ֻ�������������õ������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() �İ뾶Ϊ2��Բ����
�İ뾶Ϊ2��Բ����![]() ����������ϣ�����ֱ��
����������ϣ�����ֱ��![]() ����.
����.
(1)��Բ![]() �ķ��̡�
�ķ��̡�
(2)��Բ![]() �ϣ��Ƿ���ڵ�
�ϣ��Ƿ���ڵ�![]() ��ʹ��ֱ��
��ʹ��ֱ��![]() ��Բ
��Բ![]() �ཻ�ڲ�ͬ������
�ཻ�ڲ�ͬ������![]() ���ҡ�
���ҡ�![]() �������������ڣ������
�������������ڣ������![]() �����꼰��Ӧ�ġ�
�����꼰��Ӧ�ġ�![]() ��������������ڣ���˵������.
��������������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ������У��١��ȱ������ε������ڽǾ�Ϊ60�㡱�������⣻
�ڡ���![]() ����
����![]() ��ʵ������������⣻
��ʵ������������⣻
�ۡ�ȫ�������ε������ȡ��ķ����⣻
�ܡ���![]() ����
����![]() ���ķ�����.
���ķ�����.
����������ĸ����ǣ� ��
A. 0 B. 1 C. 2 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪��
�У���֪��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() �Ĵ�������
�Ĵ�������![]() Ϊֱ����Բ
Ϊֱ����Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣮
���㣮
��1����![]() ����Բ
����Բ![]() �ķ��̣�
�ķ��̣�
��2����֤����![]() ʼ����ij��Բ�ϣ�
ʼ����ij��Բ�ϣ�
��3���Ƿ����һ����![]() �����ڵ�
�����ڵ�![]() ����ʹ��
����ʹ��![]() Ϊ�����������ڣ��������
Ϊ�����������ڣ��������![]() �����ꣻ�������ڣ�˵�����ɣ�
�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com