
【题目】以下四个命题:①设![]() ,则
,则![]() 是
是![]() 的充要条件;②已知命题
的充要条件;②已知命题![]() 、
、![]() 、
、![]() 满足“
满足“![]() 或
或![]() ”真,“
”真,“![]() 或
或![]() ”也真,则“
”也真,则“![]() 或
或![]() ”假;③若
”假;③若![]() ,则使得
,则使得![]() 恒成立的
恒成立的![]() 的取值范围为{
的取值范围为{![]() 或
或![]() };④将边长为
};④将边长为![]() 的正方形
的正方形![]() 沿对角线
沿对角线![]() 折起,使得
折起,使得![]() ,则三棱锥
,则三棱锥![]() 的体积为
的体积为![]() .其中真命题的序号为________.
.其中真命题的序号为________.
【答案】①③④
【解析】
①中,根据对数函数的运算性质,即可判定;②中,根据复合命题的真假判定方法,即可判定;③中,令![]() ,转化为
,转化为![]() 在
在![]() 恒成立,即可求解;④中,根据几何体的结构特征和椎体的体积公式,即可求解.
恒成立,即可求解;④中,根据几何体的结构特征和椎体的体积公式,即可求解.
由题意,①中,当![]() ,根据对数函数的运算性质,可得
,根据对数函数的运算性质,可得![]() ,
,
反证,当![]() 时,可得
时,可得![]() ,所以“
,所以“![]() ”是“
”是“![]() ”成立的充要条件,所以是正确的;
”成立的充要条件,所以是正确的;
②中,若命题““![]() 或
或![]() ”真”,可得命题
”真”,可得命题![]() 中至少有一个是真命题,当
中至少有一个是真命题,当![]() 为真命题,则
为真命题,则![]() 假命题,此时若“
假命题,此时若“![]() 或
或![]() ”真,则命题
”真,则命题![]() 为真命题,所以“
为真命题,所以“![]() 或
或![]() ”真命题,所以不正确;
”真命题,所以不正确;
③中,令![]() ,则不等式
,则不等式![]() 恒成立转化为
恒成立转化为![]() 在
在![]() 恒成立,
恒成立,
则满足![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() ,所以是正确的;
,所以是正确的;
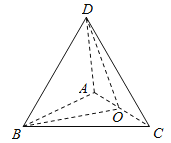
④中,如图所示,O为AC的中点,连接DO,BO,
则![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,
,
其中![]() 也是等腰直角三角形,
也是等腰直角三角形,![]() 平面
平面![]() ,
,
![]() 为三棱锥
为三棱锥![]() 的高,且
的高,且![]() ,
,
所以三棱锥![]() 的体积为
的体积为![]() ,所以是正确的,
,所以是正确的,
综上可知真命题的序号为①③④


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每卦有三根线组成(“![]() ”表示一根阳线,“
”表示一根阳线,“![]() ”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.
”表示一根阴线),从八卦中任取两卦,这两卦的六根线中恰有三根阳线和三根阴线的概率__________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,长轴长是短轴长的2倍.
,长轴长是短轴长的2倍.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 相交于
相交于![]() 两点(异于点
两点(异于点![]() ),记直线
),记直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,证明:
,证明:![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面![]() 与平面
与平面![]() 平行的充分条件可以是( )
平行的充分条件可以是( )
A.![]() 内有无穷多条直线都与
内有无穷多条直线都与![]() 平行
平行
B.直线![]() ,
,![]() ,且直线a不在
,且直线a不在![]() 内,也不在
内,也不在![]() 内
内
C.直线![]() ,直线
,直线![]() ,且
,且![]() ,
,![]()
D.![]() 内的任何一条直线都与
内的任何一条直线都与![]() 平行
平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.

(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
销售收益y(单位:万元) | 1 | 3 | 4 | 7 |
表中的数据显示,x与y之间存在线性相关关系,请将(2)的结果填入上表的空白栏,并计算y关于x的回归方程.
回归直线的斜率和截距的最小二乘法估计公式分别为 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com