
【题目】某中学为了普及奥运会知识和提高学生参加体育运动的积极性,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
(Ⅰ)在这30名学生中,甲组学生中有男生7人,乙组学生中有女生12人,试问有没有90%的把握认为成绩分在甲组或乙组与性别有关;
(Ⅱ)记甲组学生的成绩分别为x1 , x2 , …,x12 , 执行如图所示的程序框图,求输出的S的值;
(Ⅲ)竞赛中,学生小张、小李同时回答两道题,小张答对每道题的概率均为 ![]() ,小李答对每道题的概率均为
,小李答对每道题的概率均为 ![]() ,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.
,两人回答每道题正确与否相互独立.记小张答对题的道数为a,小李答对题的道数为b,X=|a﹣b|,写出X的概率分布列,并求出X的数学期望.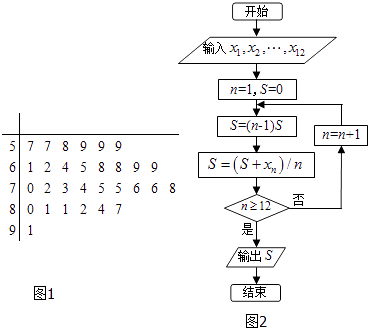
附:K2= ![]() ;其中n=a+b+c+d
;其中n=a+b+c+d
独立性检验临界表:
P(K2>k0) | 0.100 | 0.050 | 0.010 |
k0 | 2.706 | 3.841 | 6.635 |
【答案】解:(Ⅰ)作出2×2列联表:
甲组 | 乙组 | 合计 | |
男生 | 7 | 6 | 13 |
女生 | 5 | 12 | 17 |
合计 | 12 | 18 | 30 |
由列联表数据代入公式,计算得K2= 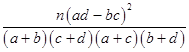 =
= ![]() ≈1.83,
≈1.83,
因为1.83<2.706,故没有90%的把握认为成绩分在甲组或乙组与性别有关;
(Ⅱ)根据程序运行的过程,得出该程序运行后输出的是求甲组数据的平均数,
所以输出S= ![]() ×(75+75+76+76+78+80+81+81+82+84+87+91)=80.5;
×(75+75+76+76+78+80+81+81+82+84+87+91)=80.5;
(Ⅲ)由已知得X的可能取值为0,1,2,
P(X=0)=(1﹣ ![]() )(1﹣
)(1﹣ ![]() )(1﹣
)(1﹣ ![]() )+
)+ ![]()
![]() (1﹣
(1﹣ ![]() )
) ![]() =
= ![]() ,
,
P(X=1)= ![]()
![]() (1﹣
(1﹣ ![]() )(1﹣
)(1﹣ ![]() )+(1﹣
)+(1﹣ ![]() )(1﹣
)(1﹣ ![]() )
) ![]() +
+ ![]()
![]()
![]() =
= ![]() ,
,
P(X=2)= ![]()
![]() (1﹣
(1﹣ ![]() )=
)= ![]() ,
,
∴X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
X的数学期望值为EX=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =
= ![]()
【解析】(Ⅰ)作2×2列联表,计算K2 , 对照数表即可得出结论;(Ⅱ)根据程序运行的过程,得出该程序运行后输出的是求平均数,求出即可;(Ⅲ)由已知得X的可能取值,计算对应的概率值,写出X的分布列,计算数学期望值.
【考点精析】根据题目的已知条件,利用离散型随机变量及其分布列的相关知识可以得到问题的答案,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】若a和b是计算机在区间(0,2)上产生的均匀随机数,则一元二次不等式ax2+4x+4b>0(a>0)的解集不是R的概率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
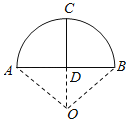
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定集合A={a1 , a2 , a3 , …,an}(n∈N* , n≥3)中,定义ai+aj(1≤i<j≤n,i,j∈N*)中所有不同值的个数为集合A两元素和的容量,用L(A)表示.若数列{an}是公差不为0的等差数列,设集合A={a1 , a2 , a3 , …,a2016},则L(A)= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,平行四边形ABCD中,AB=2AD,∠DAB=60°,M是BC的中点.将△ADM沿DM折起,使面ADM⊥面MBCD,N是CD的中点,图2所示. 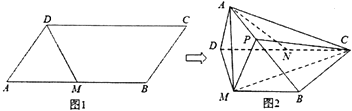
(Ⅰ)求证:CM⊥平面ADM;
(Ⅱ)若P是棱AB上的动点,当 ![]() 为何值时,二面角P﹣MC﹣B的大小为60°.
为何值时,二面角P﹣MC﹣B的大小为60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC和△ACD中,∠ACB=∠ADC=90°,∠BAC=∠CAD,⊙O是以AB为直径的圆,DC的延长线与AB的延长线交于点E.
(Ⅰ)求证:DC是⊙O的切线;
(Ⅱ)若EB=6,EC=6 ![]() ,求BC的长.
,求BC的长.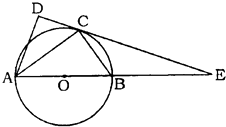
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A={x|2x2+ax+2=0},B={x|x2+3x+2a=0},A∩B={2}.
(1)求a的值及集合A、B;
(2)设集合U=A∪B,求(CuA)∪(CuB)的所有子集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com