Question

已知二面角α-l-β的大小为50°，P为空间中任意一点，则过点P且与平面α，β所成的角都是25°的直线的条数为（ ）
A．2
B．3
C．4
D．5

Answer 1

【答案】分析：利用线面角的概念及角平分线的性质，分析出所求直线二面角的平分面上，再根据线面角的大小变化确定出直线条数．
解答：解：首先给出下面两个结论
①两条平行线与同一个平面所成的角相等．
②与二面角的两个面成等角的直线在二面角的平分面上．
图1．
（1）如图1，过二面角α-l-β内任一点作棱l的垂面AOB，交棱于点O，与两半平面于OA，OB，则∠AOB为二面角α-l-β的平面角，∠AOB=50°
设OP₁为∠AOB的平分线，则∠P₁OA=∠P₁OB=25°，与平面α，β所成的角都是25°，此时过P且与OP₁平行的直线符合要求，有一条．当OP₁以O为轴心，在二面角α-l-β的平分面上转动时，OP₁与两平面夹角变小，不再会出现25°情形． 
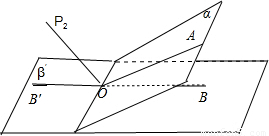
图2．
（2）如图2，设OP₂为∠AOB的补角∠AOB′，则∠P₂OA=∠P₂OB=65°，与平面α，β所成的角都是65°．当OP₂以O为轴心，在二面角α-l-β′的平分面上转动时，OP₂与两平面夹角变小，对称地在图中OP₂两侧会出现25°情形，有两条．此时过P且与OP₂平行的直线符合要求，有两条．
综上所述，直线的条数共有三条．
故选B．
点评：本题考查二面角、线面角的概念及度量．利用线面角的概念及角平分线的性质，得出所求直线的空间位置，线面角的大小变化是关键．考查空间想象、分析解决问题能力．