
【题目】某村充分利用自身资源,大力发展养殖业以增加收入.计划共投入80万元,全部用于甲、乙两个项目,要求每个项目至少要投入20万元在对市场进行调研时发现甲项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足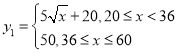 ,乙项目的收益
,乙项目的收益![]() 与投入x(单位:万元)满足
与投入x(单位:万元)满足![]() .
.
(1)当甲项日的投入为25万元时,求甲、乙两个项目的总收益;
(2)问甲、乙两个项目各投入多少万元时,总收益最大?
【答案】(1)92.5万元(2)甲、乙两个项日分别投入25万元、55万元时,总收益最大.
【解析】
(1)当甲投入25万元时,将投入的资金代入相应的解析式中,可求得两个项目的总收益;
(2)设甲投入x万元,则乙投入![]() 万元,根据范围求得总收益的函数解析式,再分段求得函数的最大值,比较后可得答案.
万元,根据范围求得总收益的函数解析式,再分段求得函数的最大值,比较后可得答案.
(1)当甲投入25万元,则乙投入55万元,甲、乙两个项目的总收益为![]() ,
,
所以甲、乙两个项日的总收益为92.5万元.
(2)设甲投入x万元,则乙投入![]() 万元,由
万元,由![]() ,解得
,解得![]() ,
,
甲项目的收益为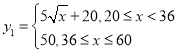 ,乙项目的收益为
,乙项目的收益为![]() ,
,
所以甲、乙两个项目的总收益为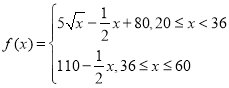 ,
,
当![]() ,
,![]() ,∴当
,∴当![]() ,即
,即![]() ,
,![]() 的最大值为92.5.
的最大值为92.5.
当![]() ,
,![]() 递减,∴当
递减,∴当![]() ,
,![]() 的最大值为92,
的最大值为92,
综上,当![]() ,
,![]() 的最大值为92.5,
的最大值为92.5,
所以甲、乙两个项日分别投入25万元、55万元时,总收益最大.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】自出生之日起,人的情绪、体力、智力等心理、生理状况就呈周期变化,变化由线为![]() .根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
.根据心理学家的统计,人体节律分为体力节律、情绪节律和智力节律三种.这些节律的时间周期分别为23天、28天、33天.每个节律周期又分为高潮期、临界日和低潮期三个阶段.以上三个节律周期的半数为临界日,这就是说11.5天、14天、16.5天分别为体力节律、情绪节律和智力节律的临界日.临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),已知小英的生日是2003年3月20日(每年按365天计算).
(1)请写出小英的体力、情绪和智力节律曲线的函数;
(2)试判断小英在2019年4月22日三种节律各处于什么阶段,当日小英是否适合参加某项体育竞技比赛?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定平面上的五个点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
,任意三点不共线.由这些点连成4条线段,每个点至少是一条线段的端点.则不同的连结方式有( ).
A. 120种 B. 125种 C. 130种 D. 135种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(1)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(2)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:

设农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程![]() =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(注:![]() =
= =
= ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com