
【题目】已知圆C:(x﹣3)2+(y﹣4)2=4
(1)若平面上有两点A(1,0),B(﹣1,0),点P是圆C上的动点,求使|AP|2+|BP|2取得最小值时点P的坐标;
(2)若Q是x轴上的动点,QM,QN分别切圆C于M,N两点,①若 ![]() ,求直线QC的方程;②求证:直线MN恒过定点.
,求直线QC的方程;②求证:直线MN恒过定点.
【答案】
(1)解:设P(x,y),由两点间的距离公式知:|AP|2+|BP|2=2(x2+y2)+2=2|OP|2+2.
又P为圆上的点,所以 ![]() ,∴(|AP|2+|BP|2)min=20
,∴(|AP|2+|BP|2)min=20
此时直线 ![]() ,由题意得:
,由题意得: 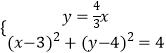 ,∴P的坐标为
,∴P的坐标为 ![]()
(2)解:①设Q(x,0),因为圆C的半径r=2,而 ![]() ,
,
则 ![]() ,
, ![]()
而|QN|=|QM|,△QMN为等边三角形.
∴|QC|2=|QN|2+|CN|2=16,∴|QC|=4,所求直线QC的方程:x=3
② ![]() ,则M,N在以QC为直径的圆上
,则M,N在以QC为直径的圆上
设Q(a,0),则以QC为直径的圆的方程: ![]()
即x2+y2﹣(a+3)x﹣4y+3a=0与圆C:x2+y2﹣6x﹣8y+21=0联立得:﹣a(x﹣3)+3x+4y﹣21=0,
故无论a取何值时,直线MN恒过定点(3,3)
【解析】(1)根据圆的标准方程,设出点P的坐标,然后利用两点间距离公式,得到|AP|2+|BP|2的表达式,即可求得P点的坐标.(2)①确定|QN|=|QM|,△QMN为等边三角形,即可求直线QC的方程;②x2+y2﹣(a+3)x﹣4y+3a=0与圆C:x2+y2﹣6x﹣8y+21=0联立得:﹣a(x﹣3)+3x+4y﹣21=0,即可证明结论.


科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD中,底面ABCD为菱形,且直线PA⊥平面ABCD,又棱PA=AB=2,E为CD的中点,∠ABC=60°.
(Ⅰ) 求证:直线EA⊥平面PAB;
(Ⅱ) 求直线AE与平面PCD所成角的正切值.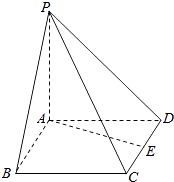
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图. 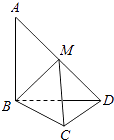
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知锐角△ABC的三个内角A,B,C的对边分别为a,b,c,且 ![]() =(a,b+c),
=(a,b+c), ![]() .
.
(1)求角A;
(2)若a=3,求△ABC面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在三棱锥S﹣ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC= ![]() ,M为AB的中点.
,M为AB的中点.
(I)证明:AC⊥SB;
(Ⅱ)求点B到平面SCM的距离.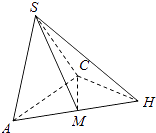
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: 
(1)求该运动员得分的中位数和平均数;
(2)估计该运动员每场得分超过10分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com