
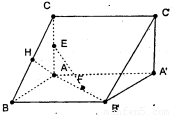
 BB'=1.结合BB'⊥平面ABC,得FI⊥平面ABC,可得FI是三棱锥F-AEH的高线.求出△AEH的面积,结合锥体体积公式,可得三棱锥F-AEH的体积,即为四面体E-FAH的体积.
BB'=1.结合BB'⊥平面ABC,得FI⊥平面ABC,可得FI是三棱锥F-AEH的高线.求出△AEH的面积,结合锥体体积公式,可得三棱锥F-AEH的体积,即为四面体E-FAH的体积. 连接B'C,
连接B'C, 取AB的中点I,连接FI
取AB的中点I,连接FI BB'=1
BB'=1 =2,可得S△AEH=
=2,可得S△AEH= S△ABC=
S△ABC=
 S△AEH×EI=
S△AEH×EI= ×
× ×1=
×1=



 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知直三棱柱ABC—A1B1C1中,△ABC为等腰直角三角形,
∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
求证:
(1)DE∥平面ABC;
(2)B1F⊥平面AEF.

查看答案和解析>>
科目:高中数学 来源:2011-2012学年陕西省宝鸡市高三教学质量检测(三)理科数学试卷(解析版) 题型:解答题
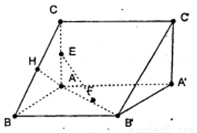
如图所示,已知直三棱柱ABC–A′B′C′,AC =AB =AA,=2,AC,AB,AA′两两垂直, E,F,H分别是AC,AB,BC的中点,
(I)证明:EF⊥AH;
(II)求平面EFC与平面BB′C′所成夹角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com