
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源:不详 题型:填空题
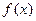 的定义域为D,若对于任意
的定义域为D,若对于任意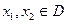 ,当
,当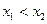 时,都有
时,都有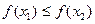 ,则称函数
,则称函数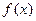 在D上为非减函数。设函数
在D上为非减函数。设函数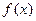 在[0,1]上为非减函数,且满足以下三个条件:
在[0,1]上为非减函数,且满足以下三个条件: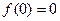 ;②
;②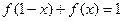 ;
;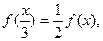
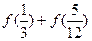 的值为
的值为 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
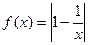 ,(x>0).
,(x>0).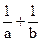 的值 ;
的值 ;  若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [
若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ ma,mb],(m≠0),求m的取值范围.
ma,mb],(m≠0),求m的取值范围. 查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
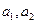 满足
满足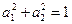 ,那么
,那么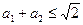 。”
。”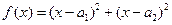 ,因为对一切实数
,因为对一切实数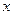 ,恒有
,恒有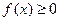 ,
,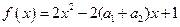 ,从而得
,从而得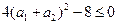 ,所以
,所以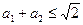 。
。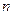 个正实数满足
个正实数满足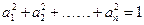 时,你可以构造函数
时,你可以构造函数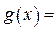 _______ ,进一步能得到的结论为 ______________ (不必证明).
_______ ,进一步能得到的结论为 ______________ (不必证明).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com