
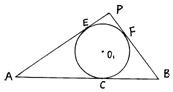
 ��ͼ����PAB�Ķ���A��BΪ���㣬PΪ���㣬������ԲO1��AB��PA��PB�ֱ������ڵ�C��E��F����$AB=2\sqrt{3}$��||AC|-|BC||=2��
��ͼ����PAB�Ķ���A��BΪ���㣬PΪ���㣬������ԲO1��AB��PA��PB�ֱ������ڵ�C��E��F����$AB=2\sqrt{3}$��||AC|-|BC||=2������ ��1������ƽ�漸�ε�֪ʶ�ɵá�||PA|-|PB||=||AC|-|BC||=2��
��2���Ե�OΪ����ԭ�㣬�߶�AB���ڵ�ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ������˫���ߵĶ��壬֪����P�Ĺ켣����A��BΪ�����˫���ߵIJ��֣�������Խ����
��3����ֱ��l��y=kx+b��k��0�����������飬��y�����ݸ���ϵ���Ĺ�ϵ�ɵã�x1x2=-$\frac{{b}^{2}+2}{2-{k}^{2}}$��x1+x2=$\frac{2kb}{2-{k}^{2}}$���ٸ�����������������ʽ�ɵ�$\overrightarrow{OG}$•$\overrightarrow{OH}$=-2k2+b2-2���ٸ��ݵ㵽ֱ�ߵľ��빫ʽ�ɵ�2k2+2=b2������֤��$\overrightarrow{OG}$•$\overrightarrow{OH}$=0����$2\overrightarrow{OM}=\overrightarrow{OG}+\overrightarrow{OH}$������֤�����۳�����
��� �⣺��1���������߳������ɵ�|PE|=|PF|��|AE|=|AC|��|BF|=|BC|��
��||PA|-|PB||=||PE|+|AE|-|PF|-|BF||=||AC|-|BC||=2��
��2���Ե�OΪ����ԭ�㣬�߶�AB���ڵ�ֱ��Ϊx�ᣬ����ƽ��ֱ������ϵ��
�ɣ�1����֪||PA|-|PB||=2��|AB|=2$\sqrt{3}$��
����˫���ߵĶ��壬֪����P�Ĺ켣����A��BΪ�����˫���ߵIJ��֣�
��2a=2��2c=2$\sqrt{3}$��
�ද��P�Ĺ켣W�ķ���x2-$\frac{{y}^{2}}{2}$=1����y��0����
��3��֤������ֱ��l��y=kx+b��k��0��
����$\left\{\begin{array}{l}{y=kx+b}\\{2{x}^{2}-{y}^{2}=2}\end{array}\right.$���ã�2-k2��x2-2kbx-b2-2=0��
��������k2��2����=b2-k2+2��0��x1x2=-$\frac{{b}^{2}+2}{2-{k}^{2}}$��x1+x2=$\frac{2kb}{2-{k}^{2}}$��
��$\overrightarrow{OG}$•$\overrightarrow{OH}$=x1x2+y1y2=��k2+1��x1x2+kb��x1+x2��+b2=-2k2+b2-2��
��d=$\sqrt{2}$=$\frac{|b|}{\sqrt{{k}^{2}+1}}$��
��2k2+2=b2��
��$\overrightarrow{OG}$•$\overrightarrow{OH}$=0��
��$2\overrightarrow{OM}=\overrightarrow{OG}+\overrightarrow{OH}$��
��$2|\overrightarrow{OM}|=|\overrightarrow{GH}|$��
���� ���⿼����˫���ߵķ��̵���ֱ�ߺ�˫���ߵ�λ�ù�ϵ���Լ��������������͵㵽ֱ�ߵľ��빫ʽ�������е��⣮


 �������ϵ�д�
�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{17}}{3}$ | B�� | $\frac{\sqrt{10}}{2}$ | C�� | $\sqrt{13}$ | D�� | $\frac{\sqrt{58}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{\sqrt{3}+1}{2}$ | B�� | $\sqrt{6}$+1 | C�� | $\sqrt{3}$+1 | D�� | $\frac{\sqrt{3}+1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{1}{16}$��0�� | B�� | ��1��0�� | C�� | ��0��$\frac{1}{16}$�� | D�� | ��0��1 �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���a��b����ô$\frac{a}{c}$��$\frac{b}{c}$ | B�� | ���ac��bc����ôa��b | ||
| C�� | ���a��b��c��d����ôa-c��b-d | D�� | ���a��b����ôa-c��b-c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p�ģ�?q�� | B�� | ��?p����q | C�� | ��?p���ģ�?q�� | D�� | p��q |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | $\frac{7}{4}$ | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com