
【题目】对于无穷数列![]() ,
,![]() ,记
,记![]() ,
,![]() ,若同时满足条件①
,若同时满足条件①![]() ,
,![]() 均单调递增;②
均单调递增;②![]() 且
且![]() ,则称
,则称![]() ,
,![]() 是无穷互补数列.
是无穷互补数列.
(1)若![]() ,
,![]() ,试判断数列
,试判断数列![]() ,
,![]() 是否为无穷互补数列,并说明理由;
是否为无穷互补数列,并说明理由;
(2)若![]() ,且
,且![]() ,
,![]() 是无穷互补数列,求数列
是无穷互补数列,求数列![]() 前
前![]() 项的和.
项的和.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了让居民了解垃圾分类,养成垃圾分类的习惯,让绿色环保理念深入人心.某市将垃圾分为四类:可回收物,餐厨垃圾,有害垃圾和其他垃圾.某班按此四类由10位同学组成四个宣传小组,其中可回收物与餐厨垃圾宣传小组各有2位同学,有害垃圾与其他垃圾宣传小组各有3位同学.现从这10位同学中选派5人到某小区进行宣传活动,则每个宣传小组至少选派1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为![]() 和
和![]() 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形.该矩形长为![]() ,宽为内接正方形的边长
,宽为内接正方形的边长![]() .由刘徽构造的图形还可以得到许多重要的结论,如图3.设
.由刘徽构造的图形还可以得到许多重要的结论,如图3.设![]() 为斜边
为斜边![]() 的中点,作直角三角形
的中点,作直角三角形![]() 的内接正方形对角线
的内接正方形对角线![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,则下列推理正确的是( )
,则下列推理正确的是( )
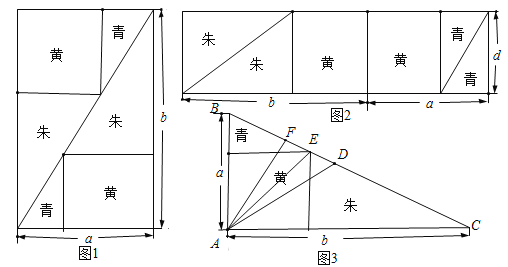
①由图1和图2面积相等得![]() ;
;
②由![]() 可得
可得![]() ;
;
③由![]() 可得
可得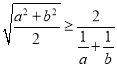 ;
;
④由![]() 可得
可得![]() .
.
A.①②③④B.①②④C.②③④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列![]() ,若存在常数M,使得对任意
,若存在常数M,使得对任意![]() ,
,![]() 与
与![]() 中至少有一个不小于M,则记作
中至少有一个不小于M,则记作![]() ,那么下列命题正确的是( ).
,那么下列命题正确的是( ).
A.若![]() ,则数列
,则数列![]() 各项均大于或等于M;
各项均大于或等于M;
B.若![]() ,则
,则![]() ;
;
C.若![]() ,
,![]() ,则
,则![]() ;
;
D.若![]() ,则
,则![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 是正方形,顶点
是正方形,顶点![]() 在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为
在底面的射影是底面的中心,且各顶点都在同一球面上,若该四棱锥的侧棱长为![]() ,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:
,体积为4,且四棱锥的高为整数,则此球的半径等于( )(参考公式:![]() )
)
A. 2B. ![]() C. 4D.
C. 4D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(x,y)是平面内的动点,定点F(1,0),定直线l:x=﹣1与x轴交于点E,过点P作PQ⊥l于点Q,且满足![]()
![]()
![]()
![]()
![]() .
.
(1)求动点P的轨迹t的方程;
(2)过点F作两条互相垂直的直线,分别交曲线t于点A,B,和点C,D.设线段AB和线段CD的中点分别为M和N,记线段MN的中点为K,点O为坐标原点,求直线OK的斜率k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com