
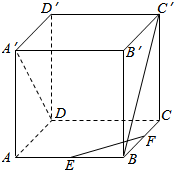
 如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:
如图,正方体ABCD-A′B′C′D′的棱长为a,E,F分别是棱AB,BC的中点,求:分析 (1)根据图形,BC∥A′D′,从而得出∠EFB为所求异面直线所成角,并知道该角为45°;
(2)连接AD′,从而AD′∥BC′,而AD′⊥A′D,这样便可得出要求的异面直线所成角的大小;
(3)可连接AC,CD′,则∠CAD′便是所求的异面直线所成的角,并能得出该角.
解答  解:(1)BC∥A′D′;
解:(1)BC∥A′D′;
∴∠EFB为异面直线A′D′与EF所成角;
∵E,F分别是棱AB,BC的中点;
∴∠EFB=45°;
即异面直线A′D′与EF所成角的大小为45°;
(2)如图,
连接AD′,设交A′D于O,则AD′∥BC′;
∴∠AOD为异面直线A′D与BC′所成角,且∠AOD=90°;
即异面直线A′D与BC′所成角的大小为90°;
(3)连接AC,CD′,则AC∥EF;
∴∠CAD′为异面直线BC′与EF所成角,且△ACD′为等边三角形;
∴∠CAD′=60°;
即异面直线BC′与EF所成角的大小为60°.
点评 考查异面直线所成的角的定义,以及求异面直线所成角的方法和过程.


科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{π}{12}$ | B. | 1-$\frac{π}{10}$ | C. | 1-$\frac{π}{6}$ | D. | 1-$\frac{π}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
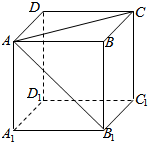 在如图所示的正方体ABCD-A1B1C1D1中,求:
在如图所示的正方体ABCD-A1B1C1D1中,求:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
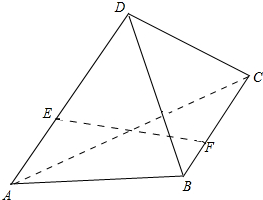 如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.
如图,AB和CD是两条异面直线,AB=CD=3,E,F分别为线段AD,BC上的点,且$\frac{AE}{ED}$=$\frac{BF}{FC}$=$\frac{1}{2}$,EF=$\sqrt{7}$,求AB和CD所成的角.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+4y-2=0 | B. | x-4y+2=0 | C. | 4x+2y-1=0 | D. | 4x-2y-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
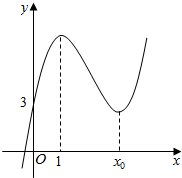 已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).
已知函数f(x)=ax3+bx2+(c-3a-2b)x+d(a>0)的图象如图所示,该函数的单调增区间为(-∞,1)和(x0,+∞),单调减区间为(1,x0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com