
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在
在![]() 上为增函数,求实数
上为增函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)当![]() 时,求函数的导数,利用导数的几何意义即可求曲线
时,求函数的导数,利用导数的几何意义即可求曲线![]() 在
在![]() 处的切线斜率,由点斜式可得结果;(2)函数
处的切线斜率,由点斜式可得结果;(2)函数![]() 在
在![]() 上为增函数,等价于对任意x,
上为增函数,等价于对任意x,![]() 上恒成立,
上恒成立,![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,利用导数研究函数的单调性,由单调性求出
,利用导数研究函数的单调性,由单调性求出![]() 的最小值,即可求
的最小值,即可求![]() 的取值范围.
的取值范围.
(1)当a=1时, ![]() ,
,
∴f(1)=-e-![]() ×12+2×1=
×12+2×1=![]() -e,
-e,
又f ′(x)=-ex-x+2,
∴f ′(1)=-e-1+2=1-e,
∴曲线y=f(x)在x=1处的切线方程为y-![]() =(1-e)(x-1),
=(1-e)(x-1),
即所求切线方程为:(1-e)x-y+![]() =0 .
=0 .
(2)∵函数![]() 在R上是增函数,
在R上是增函数,
∴f ′(x)≥0在R上恒成立,
∴-aex-x+2≥0在R上恒成立,即a≤![]() 在R上恒成立,
在R上恒成立,
令g(x)=![]() ,则g′(x)=
,则g′(x)=![]() ,
,
令g′(x)=0,解得x=3,
当x变化时,g(x)、g′(x)的变化情况如下表:
x | (-∞,3) | 3 | (3,+∞) |
g′(x) | - | 0 | + |
g(x) | 减 |
| 增 |
∴函数g(x)在x=3处取得极小值![]() ,即g(x)min=
,即g(x)min=![]() ,
,
∴a≤![]() ,
,
∴实数a的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】某商场为一种跃进商品进行合理定价,将该商品按事先拟定的价格进行试销,得到如下数据:
单位 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)按照上述数据,求四归直线方程![]() ,其中
,其中![]() ,
,![]() ;
;
(2)预计在今后的销售中,销量与单位仍然服从(Ⅰ)中的关系,若该商品的成本是每件7.5元,为使商场获得最大利润,该商品的单价应定为多少元?(利润=销售收入﹣成本)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,已知a1=1,a2=a,an+1=k(an+an+2)对任意n∈N*都成立,数列{an}的前n项和为Sn .
(1)若{an}是等差数列,求k的值;
(2)若a=1,k=﹣ ![]() ,求Sn;
,求Sn;
(3)是否存在实数k,使数列{am}是公比不为1的等比数列,且任意相邻三项am , am+1 , am+2按某顺序排列后成等差数列?若存在,求出所有k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,椭圆:![]() 的离心率为
的离心率为![]() ,y轴于椭圆相交于A、B两点,
,y轴于椭圆相交于A、B两点,![]() ,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
,C、D是椭圆上异于A、B的任意两点,且直线AC、BD相交于点M,直线AD、BC相交于点N.
![]() 求椭圆的方程;
求椭圆的方程;
![]() 求直线MN的斜率.
求直线MN的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.求证: 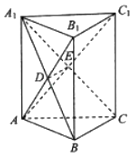
(1)DE∥平面B1BCC1;
(2)平面A1BC⊥平面A1ACC1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,∠ACB=90°,CC1⊥底面ABC,AC=BC=CC1=2,D,E,F分别是棱AB,BC,B1C1的中点,G是棱BB1上的动点. 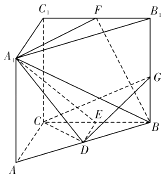
(1)当 ![]() 为何值时,平面CDG⊥平面A1DE?
为何值时,平面CDG⊥平面A1DE?
(2)求平面AB1F与平面AD1E所成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=8x,圆M:(x﹣2)2+y2=4,点N为抛物线E上的动点,O为坐标原点,线段ON的中点P的轨迹为曲线C.
(1)求曲线C的方程;
(2)点Q(x0 , y0)(x0≥5)是曲线C上的点,过点Q作圆M的两条切线,分别与x轴交于A,B两点,求△QAB面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com