圆心在y轴上,且与直线y=x相切于点(1,1)的圆的方程为 .
【答案】
分析:由圆心在y轴上,设圆心坐标为(0,b),半径为r,表示出圆的标准方程,由直线y=x与圆相切于点(1,1),得到圆心与此点的连线与y=x垂直,根据两点的坐标表示出此直线的斜率,利用两直线垂直时斜率的乘积为-1列出关于b的关系式,再将切点的坐标代入圆的方程得到关于b与r的关系式,联立两关系式求出b与r的值,即可确定出圆的方程.
解答:解:设圆心为(0,b),半径为r,则圆的方程为x
2+(y-b)
2=r
2,
依题意有
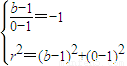
,
解得
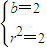
,
所以圆的方程为x
2+(y-2)
2=2.
故答案为:x
2+(y-2)
2=2
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,两直线垂直时斜率满足的关系,切线的性质,以及直线斜率的求法,当直线与圆相切时,圆心到直线的距离等于圆的半径,且切线垂直于过切点的半径.

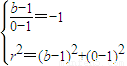 ,
,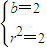 ,
,

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案