
| A. | ∅ | B. | {(1,1)} | C. | {(x,y)|x+y-2=0} | D. | {(x,y)|3x-2y-1=0} |
分析 先根据集合A,得到直线l恒过点(1,1),设圆x2+y2=2过点(1,1)的切线方程为kx-y-k+1=0,由此能示出A∩B.
解答 解:(m+3)x+(m-2)y-1-2m=0,即m(x+y-2)m+3x-2y-1=0,
∴$\left\{\begin{array}{l}{x+y-2=0}\\{3x-2y-1=0}\end{array}\right.$,
解得x=1,y=1,
∴直线l恒过点(1,1),
设圆x2+y2=2过点(1,1)的切线方程为:y-1=k(x-1),即kx-y-k+1=0,
则$\frac{|-k+1|}{\sqrt{{k}^{2}+1}}=\sqrt{2}$,整理,得:k2+2k+1=0,解得k=-1,
∴切线方程为:-x-y+2=0,即x+y-2=0.
∴A∩B={(x,y)|x+y-2=0}.
故选:C.
点评 本题借助集合的思想,考查了直线恒过定点以及曲线的切线方程,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)是奇函数 | B. | π为f(x)的最小正周期 | ||
| C. | f(x)的对称轴方程为x=kπ(k∈Z) | D. | f(x)的值域为[cos1,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
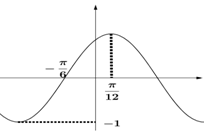 已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )
已知f(x)=Asin(ωx+φ)(A>0ω>0,$|φ|<\frac{π}{2}$,x∈R)在一个周期的图象如图所示,当$f(x)=\frac{1}{2}$时,$cos(2x-\frac{π}{6})$=( )| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
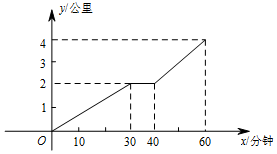 从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:
从甲同学家到乙同学家的中途有一个公园,甲、乙两家离公园入口都是2公里,甲从10点钟出发前往乙同学家,如图所示是甲同学从自己家出发到乙家经过的路程y(公里)和时间x(分钟)的关系.根据图象,回答下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com