
某企业生产某种商品 吨,此时所需生产费用为(
吨,此时所需生产费用为(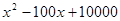 )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为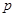 万元,这里
万元,这里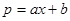 (
( 为常数,
为常数,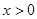 )
)
(1)为了使这种商品的生产费用平均每吨最低,那么这种商品的产量应为多少吨?
(2)如果生产出来的商品能全部卖完,当产量是120吨时企业利润最大,此时出售价格是每吨160万元,求 的值.
的值.
(1)100吨;(2)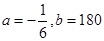 .
.
解析试题分析:这是函数应用题问题,解决问题的方法是列出函数关系式,然后借助函数的性质得出结论.这种问题的函数式其实在题中已经有提示,我们只要充分利用题目提供的信息,就可以得到解法.显然本题要建立生产商品的平均费用与商品产量之间的函数式,已知条件是生产某种商品 吨,此时所需生产费用为(
吨,此时所需生产费用为(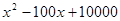 )万元,因此平均费用就是
)万元,因此平均费用就是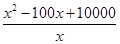 ,这就是所求函数式;(2)当产量是120吨时企业利润最大,解决这个问题要建立利润与产量之间的函数式,从实际出发,我们知道利润等于收入减去成本,因此此题中利润
,这就是所求函数式;(2)当产量是120吨时企业利润最大,解决这个问题要建立利润与产量之间的函数式,从实际出发,我们知道利润等于收入减去成本,因此此题中利润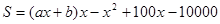 ,这是关于
,这是关于 的二次函数,已知条件转化为当
的二次函数,已知条件转化为当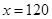 时,
时, 最大,且此时销售单价
最大,且此时销售单价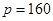 ,故问题得解.
,故问题得解.
试题解析:(1)设生产平均费用为y元,(1分)
由题意可知y=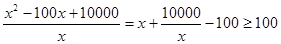 ;(5分)
;(5分)
当且仅当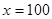 时等号成立,(6分)
时等号成立,(6分)
所以这种商品的产量应为100吨.(7分)
(2)设企业的利润为S元,有题意可知(7分)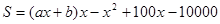
=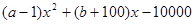 (3分)
(3分)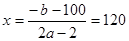 又由题意可知120
又由题意可知120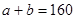 (5分)
(5分)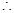
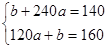
 (6分)
(6分)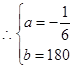 (7分)
(7分)
考点:函数的应用.


科目:高中数学 来源: 题型:解答题
设 ,
, .
.
(Ⅰ)证明: ;
;
(Ⅱ)求证:在数轴上,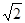 介于
介于 与
与 之间,且距
之间,且距 较远;
较远;
(Ⅲ)在数轴上,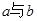 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数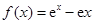 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证: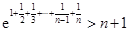
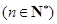 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数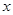 ,若存在常数
,若存在常数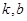 ,使得
,使得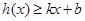 和
和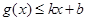 都成立,则称直线
都成立,则称直线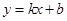 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数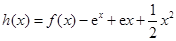 ,
,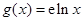 ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出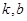 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
运货卡车以每小时 千米的速度匀速行驶130千米
千米的速度匀速行驶130千米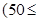
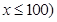 (单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用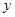 关于
关于 的表达式;
的表达式;
(2)当 为何值时,这次行车的总费用最低,并求出最低费用的值.
为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量 毫克)与时间
毫克)与时间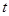 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后, 与
与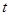 的函数关系式为
的函数关系式为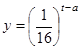 (
(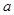 为常数),如图所示,根据图中提供的信息,回答下列问题:
为常数),如图所示,根据图中提供的信息,回答下列问题: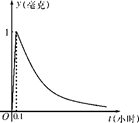
(1)求从药物释放开始,每立方米空气中的含药量 (毫克)与时间
(毫克)与时间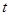 (小时)之间的函数关系式;
(小时)之间的函数关系式;
(2)据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室.那从药物释放开始,至少需要经过多少小时后,学生才能回到教室?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com