
【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如下表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为犹豫与否与性别有关?请说明理由.
的把握认为犹豫与否与性别有关?请说明理由.
犹豫 | 不犹豫 | 总计 | |
男性青年 | |||
女性青年 | |||
总计 | 1800 |
参考公式:![]()
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的顶点为坐标原点,焦点
的顶点为坐标原点,焦点![]() 在
在![]() 轴的正半轴上,过焦点
轴的正半轴上,过焦点![]() 作斜率为
作斜率为![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求抛物线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 分别交准线
分别交准线![]() 于点
于点![]() ,问:在
,问:在![]() 轴的正半轴上是否存在定点
轴的正半轴上是否存在定点![]() ,使
,使![]() ,若存在,求出定点
,若存在,求出定点![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=
,AB=BC=![]() AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.

(Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的年收益与投资额成正比,投资股票等风险型产品的年收益与投资额的算术平方根成正比.已知投资1万元时两类产品的年收益分别为0.125万元和0.5万元(如图).

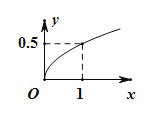
(1)分别写出两种产品的年收益与投资额的函数关系式;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大年收益,其最大年收益是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 内一定点,过
内一定点,过![]() 作两条直线交抛物线于
作两条直线交抛物线于![]() ,且
,且![]() 分别是线段
分别是线段![]() 的中点.
的中点.
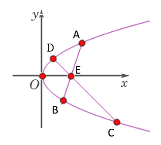
(1)当![]() 时,求△
时,求△![]() 的面积的最小值;
的面积的最小值;
(2)若![]() 且
且![]() ,证明:直线
,证明:直线![]() 过定点,并求定点坐标。
过定点,并求定点坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com