
【题目】已知函数![]() (
(![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的最小值;
的最小值;
(2)若![]() 时,
时,![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场计划销售某种产品,现邀请生产该产品的甲、乙两个厂家进场试销10天,两个厂家提供的返利方案如下:甲厂家每天固定返利70元,且每卖出一件产品厂家再返利2元;乙厂家无固定返利,卖出40件以内(含40件)的产品,每件产品厂家返利4元,超出40件的部分每件返利6元.经统计,两个厂家10天的试销情况茎叶图如下:

(Ⅰ)现从厂家试销的10天中抽取两天,求这两天的销售量都大于40的概率;
(Ⅱ)若将频率视作概率,回答以下问题:
(ⅰ)记乙厂家的日返利额为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
(ⅱ)商场拟在甲、乙两个厂家中选择一家长期销售,如果仅从日返利额的角度考虑,请利用所学的统计学知识为商场做出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
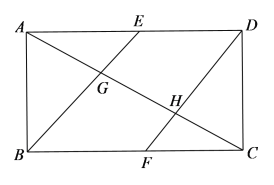
【题目】如图,一张矩形白纸![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,现分别将
的中点,现分别将![]() ,
,![]() 沿
沿![]() ,DF折起,且
,DF折起,且![]() 、
、![]() 在平面
在平面![]() 同侧,下列命题正确的是_________(写出所有正确命题的序号)
同侧,下列命题正确的是_________(写出所有正确命题的序号)
①平面![]() 平面
平面![]() 时,
时,![]()
②当平面![]() 平面
平面![]() 时,
时,![]() 平面
平面![]()
③当![]() 、
、![]() 重合于点
重合于点![]() 时,
时,![]()
④当![]() 、
、![]() 重合于点
重合于点![]() 时,三棱锥
时,三棱锥![]() 的外接球的半径为
的外接球的半径为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线![]() ,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
,以平面直角坐标系xOy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:p(2cosθ-sinθ)=6.
(1)试写出直线l的直角坐标方程和曲线C1的参数方程;
(2)在子曲线C1上求一点P,使点P到直线l的距离最大,并求出此最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,直线
,直线![]() ,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
,动圆P与圆M相外切,且与直线l相切.设动圆圆心P的轨迹为E.
(1)求E的方程;
(2)若点A,B是E上的两个动点,O为坐标原点,且![]() ,求证:直线AB恒过定点.
,求证:直线AB恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快餐连锁店招聘外卖骑手,该快餐连锁店提供了两种日工资方案:方案①:规定每日底薪50元,快递业务每完成一单提成3元;方案②:规定每日底薪100元,快递业务的前44单没有提成,从第45单开始,每完成一单提成5元.该快餐连锁店记录了每天骑手的人均业务量.现随机抽取100天的数据,将样本数据分为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七组,整理得到如图所示的频率分布直方图.
七组,整理得到如图所示的频率分布直方图.
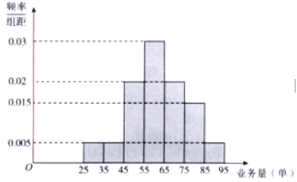
(1)随机选取一天,估计这一天该连锁店的骑手的人均日快递业务量不少于65单的概率;
(2)若骑手甲、乙选择了日工资方案①,丙、丁选择了日工资方案②.现从上述4名骑手中随机选取2人,求至少有1名骑手选择方案①的概率;
(3)若从人均日收入的角度考虑,请你利用所学的统计学知识为新聘骑手做出日工资方案的选择,并说明理由.(同组中的每个数据用该组区间的中点值代替)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com