
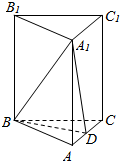
 如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.
如图,在正三棱柱ABC-A1B1C1中,侧棱与底面的边长都是2,D是AC的中点.分析 (1)在正三棱柱ABC-A1B1C1中,D是AC的中点.可得BD⊥AC,AA1⊥底面ABC,于是AA1⊥BD,BD⊥平面ACC1A1,即可证明.
(2)如图所示,建立空间直角坐标系.取平面AA1C1C的法向量为$\overrightarrow{m}$=(1,0,0).设直线BA1与平面AA1C1C所成角为θ.利用sinθ=$|cos<\overrightarrow{{A}_{1}B},\overrightarrow{m}>|$=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{m}|}{|\overrightarrow{{A}_{1}B}||\overrightarrow{m}|}$,即可得出.
(3)由已知可得:点A1到平面ABC的距离d=AA1=2.利用${V}_{{A}_{1}-ABD}$=$\frac{1}{3}d•{S}_{△ABD}$,即可得出.
(4)设点A到平面A1BD的距离为h.利用${V}_{A-{A}_{1}BD}$=${V}_{{A}_{1}-ABD}$,即可得出.
解答 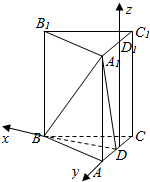 (1)证明:在正三棱柱ABC-A1B1C1中,D是AC的中点.
(1)证明:在正三棱柱ABC-A1B1C1中,D是AC的中点.
∴BD⊥AC,AA1⊥底面ABC,
∴AA1⊥BD,
又AC∩AA1=A,
∴BD⊥平面ACC1A1,
∴BD⊥A1D.
(2)解:如图所示,建立空间直角坐标系.
B($\sqrt{3}$,0,0),A1(0,1,2).
$\overrightarrow{{A}_{1}B}$=$(\sqrt{3},-1,-2)$,取平面AA1C1C的法向量为$\overrightarrow{m}$=(1,0,0).
设直线BA1与平面AA1C1C所成角为θ.
则sinθ=$|cos<\overrightarrow{{A}_{1}B},\overrightarrow{m}>|$=$\frac{|\overrightarrow{{A}_{1}B}•\overrightarrow{m}|}{|\overrightarrow{{A}_{1}B}||\overrightarrow{m}|}$=$\frac{\sqrt{3}}{\sqrt{8}}$=$\frac{\sqrt{6}}{4}$.
∴cosθ=$\sqrt{1-si{n}^{2}θ}$=$\frac{\sqrt{10}}{4}$.
(3)解:∵AA1⊥底面ABC,∴点A1到平面ABC的距离d=AA1=2.
又S△ABD=$\frac{1}{2}BD•AD$=$\frac{1}{2}×\sqrt{3}×1$=$\frac{\sqrt{3}}{2}$.
∴${V}_{{A}_{1}-ABD}$=$\frac{1}{3}d•{S}_{△ABD}$=$\frac{1}{3}×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{3}$.
(4)解:在Rt△ADA1,A1D=$\sqrt{A{A}_{1}^{2}+A{D}^{2}}$=$\sqrt{5}$.
由(1)可知:BD⊥A1D.
∴${S}_{△{A}_{1}BD}$=$\frac{1}{2}BD•{A}_{1}D$=$\frac{1}{2}×\sqrt{3}×\sqrt{5}$=$\frac{\sqrt{35}}{2}$.
设点A到平面A1BD的距离为h.
则${V}_{A-{A}_{1}BD}$=${V}_{{A}_{1}-ABD}$
∴$\frac{1}{3}•h•{S}_{△{A}_{1}BD}$=$\frac{\sqrt{3}}{3}$,
∴h=$\frac{\sqrt{3}}{\frac{\sqrt{35}}{2}}$=$\frac{2\sqrt{105}}{35}$.
点评 本题考查了空间位置关系、空间角、体积计算,考查了推理能力与计算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
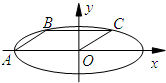 如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴长为6,点A为左顶点,B,C在椭圆E上,若四边形OABC位平行四边形,且∠OAB=30°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,3] | B. | (-∞,3] | C. | (0,3] | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
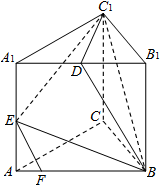 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\frac{4\sqrt{3}}{3}$ | C. | 2 | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com