
【题目】(12分)若数列{an}是的递增等差数列,其中的a3=5,且a1,a2,a5成等比数列,
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前项的和Tn.
,求数列{bn}的前项的和Tn.
(3)是否存在自然数m,使得![]() <Tn<
<Tn<![]() 对一切n∈N*恒成立?若存在,求出m的值;
对一切n∈N*恒成立?若存在,求出m的值;
若不存在,说明理由.
【答案】(1) an= 2n﹣1;(2)![]() (1﹣
(1﹣![]() )=
)=![]() ;(3)存在;理由见解析.
;(3)存在;理由见解析.
【解析】试题分析:(1)由于{![]() }为等差数列,
}为等差数列, ![]() ,
,![]() ,
,![]() ,
,![]() 成等比数列,可设出数列{
成等比数列,可设出数列{![]() }的公差为
}的公差为![]() ,列方程组即可求出
,列方程组即可求出![]() ;(2)在求出{
;(2)在求出{![]() }的通项公式后,求出{
}的通项公式后,求出{![]() }的通项公式,再应用裂项相消法即可求
}的通项公式,再应用裂项相消法即可求![]() ;(3)需先求Tn的值域,要使得
;(3)需先求Tn的值域,要使得![]() 恒成立,则需区间(
恒成立,则需区间(![]() )包含Tn的值域即可.
)包含Tn的值域即可.
试题解析:
(1)在等差数列中,设公差为d≠0,
由题意![]() ,∴
,∴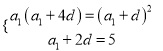 ,解得
,解得![]() .
.
∴an=a1+(n﹣1)d=1+2(n﹣1)=2n﹣1.
(2)由(1)知,an=2n﹣1.
则bn=![]()
所以Tn=![]()
(3)Tn+1﹣Tn=![]() ,
,
∴{Tn}单调递增,∴Tn≥T1=![]() .∵Tn=
.∵Tn=![]() ∴
∴![]() ≤Tn<
≤Tn<![]() , 使得
, 使得![]() 恒成立,只需
恒成立,只需
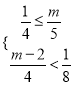 解之得
解之得![]() ,又因为m是自然数,∴m=2.
,又因为m是自然数,∴m=2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知一个动圆与已知圆Q1:(x+2)2+y2=![]() 外切,与圆Q2:(x-2)2+y2=
外切,与圆Q2:(x-2)2+y2=![]() 内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线
内切,(1) 试求这个动圆圆心的轨迹方程;(2)设直线![]() 与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线
与(1)中动圆圆心轨迹交于A、B两点,坐标原点O到直线![]() 的距离为
的距离为![]() ,求△AOB面积的最大值。
,求△AOB面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , S7=0,a3﹣2a2=12.
(1)求数列{an}的通项公式;
(2)求Sn﹣15n+50的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
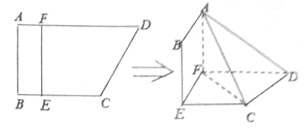
【题目】如图,四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别在
分别在![]() 上,
上, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.
(1)当![]() ,是否在折叠后的
,是否在折叠后的![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 点位置,若不存在,说明理由;
点位置,若不存在,说明理由;
(2)设![]() ,问当
,问当![]() 为何值时,三棱锥
为何值时,三棱锥![]() 的体积有最大值?并求出这个最大值.
的体积有最大值?并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“大众创业,万众创新”是李克强总理在本届政府工作报告中向全国人民发出的口号.某生产企业积极响应号召,大力研发新产品.为了对新研发的一批产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如下表所示:
,如下表所示:

已知![]() .
.
(1)求出![]() 的值;
的值;
(2)已知变量![]() ,
, ![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (件)关于试销单价
(件)关于试销单价![]() (元)的线性回归方程
(元)的线性回归方程![]() ;
;
(3)用![]() 表示用正确的线性回归方程得到的与
表示用正确的线性回归方程得到的与![]() 对应的产品销量的估计值.当销售数据
对应的产品销量的估计值.当销售数据![]() 的残差的绝对值
的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
称为一个“好数据”.现从6个销售数据中任取2个,求抽取的2个销售数据中至少有1个是“好数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)在数列![]() 中,对于任意
中,对于任意![]() ,等式
,等式![]()
成立,其中常数![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证:数列![]() 为等比数列;
为等比数列;
(Ⅲ)如果关于n的不等式![]() 的解集为
的解集为
![]() ,求b和c的取值范围.
,求b和c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点为极点,以x轴的非负半轴为极轴建立极坐标系,已知曲线C的参数方程为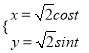 (t为参数)
(t为参数) 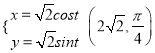 .
.
(1)若曲线C在点(1,1)处的切线为l,求l的极坐标方程;
(2)若点A的极坐标为![]() ,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
,且当参数t∈[0,π]时,过点A的直线m与曲线C有两个不同的交点,试求直线m的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的最小二乘法估计公式分别为:![]() =
=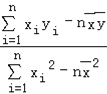 ,
,![]() =
=![]() ﹣
﹣![]()
![]() ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com