
设定义在R的函数![]() ,
,![]() R. 当
R. 当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,且函数
,且函数![]() 的图象关于点
的图象关于点![]() 对称.
对称.
(I)求函数![]() 的表达式;
的表达式;
(II)判断函数![]() 的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间
的图象上是否存在两点,使得以这两点为切点的切线互相垂直,且切点的横坐标在区间![]() 上,并说明理由;
上,并说明理由;
![]() (III)设
(III)设![]() ,
,![]() (
(![]() ),求证:
),求证:![]() .
.
(I)![]() .
.
(II)两点的坐标分别为![]() 或
或![]() .
.
(III)见解析
(I)将函数![]() 的图象向右平移一个单位得到函数
的图象向右平移一个单位得到函数![]() 的图象,
的图象,
∴ 函数![]() 的图象关于点
的图象关于点![]() 对称,即
对称,即![]() 为奇函数.
为奇函数.
∴![]() . ……………………………..2分
. ……………………………..2分
由题意可得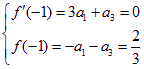 ,解得
,解得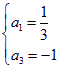 .
.
∴![]() . ……………………………..4分
. ……………………………..4分
![]() (II)存在满足题意的两点. ……………………………..6分
(II)存在满足题意的两点. ……………………………..6分
由(I)得![]() .
.
假设存在两切点![]() ,
,![]() ,且
,且![]() .
.
则![]() .
.
∵![]() ,∴
,∴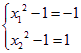 或
或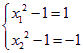 ,
,
即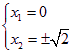 或
或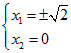 .
.
从而可求得两点的坐标分别为![]() 或
或![]() .
.
…………………………….9分
(III)∵当![]() 时,
时,![]() ,∴
,∴ ![]() 在
在![]() 上递减.
上递减.
由已知得![]() ,∴
,∴![]() ,即
,即![]() .
.
……………………………..11分
又![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上递增,
上递增,![]() 在
在![]() 上递减.
上递减.
∵![]() ,∴
,∴![]() .
.
∵![]() ,且
,且![]() ,
,
∴![]() . ……………………………13分
. ……………………………13分
![]() ∴
∴![]() . ………………………..14分
. ………………………..14分


科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 4 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 2 |
| A、1 | ||
B、2(
| ||
C、
| ||
D、3(
|
查看答案和解析>>
科目:高中数学 来源:2010-2011学年度江苏省连云港市赣榆高级中学高三暑期检测数学试卷(解析版) 题型:填空题
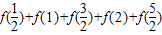 = .
= .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com