
分析 利用数列递推关系、“裂项求和”方法即可得出.
解答 解:∵${S_n}=6n-{n^2}$,
∴a1=S1=5;n≥2时,an=Sn-Sn-1=6n-n2-[6(n-1)-(n-1)2]=7-2n.n=1时也成立.
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(7-2n)(5-2n)}$=-$\frac{1}{2}(\frac{1}{2n-5}-\frac{1}{2n-7})$.
∴数列 $\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前20项和=-$\frac{1}{2}[(-\frac{1}{3}+\frac{1}{5})$+$(-1-\frac{1}{-3})$+$(1-\frac{1}{-1})$+…+$(\frac{1}{35}-\frac{1}{33})]$
=-$\frac{1}{2}(\frac{1}{5}+\frac{1}{35})$
故答案为:-$\frac{4}{35}$.
点评 本题考查了数列递推关系、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
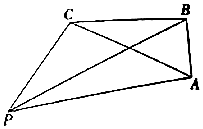 如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.
如图,有一码头P和三个岛屿A,B,C,PC=30$\sqrt{3}$n mile,PB=90n mile,AB=30n mile,∠PCB=120°,∠ABC=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$或 2 | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2018,-2016) | B. | (-∞,-2016) | C. | (-2019,-2016) | D. | (-∞,-2019) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
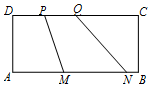 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com