
【题目】已知△ABC的三个内角A,B,C的对边分别是a,b,c,且bcosC=(2a﹣c)cosB.
(1)求角B.
(2)若 ![]() ,△ABC的周长为
,△ABC的周长为 ![]() ,求△ABC的面积.
,求△ABC的面积.
【答案】
(1)解:∵△ABC的三个内角A,B,C的对边分别是a,b,c,
且bcosC=(2a﹣c)cosB,
∴bcosC+ccosB=2acosB.
∴由正弦定理得:sinBcosC+sinCcosB=2sinAcosB,
∴sin(B+C)=2sinAcosB,∴sinA=2sinAcosB,
∴cosB= ![]() ,
,
∵B∈(0,π),∴B= ![]() .
.
(2)解:∵ ![]() ,△ABC的周长为
,△ABC的周长为 ![]() ,∴a+c=7,
,∴a+c=7,
由余弦定理得:13=a2+c2﹣2accosB=a2+c2﹣ac,
(a+c)2=a2+c2+2ac=a2+c2﹣ac+3ac=13+3ac=49,
解得ac=12,
∴△ABC的面积 ![]() =
= ![]() =3
=3 ![]() .
.
【解析】(1)由正弦定理得:sinBcosC+sinCcosB=2sinAcosB,再由正弦加法定理、诱导公式得sinA=2sinAcosB,从而cosB= ![]() ,由此能求出角B.(2)求出a+c=7,再由余弦定理得ac=12,由此能求出△ABC的面积.
,由此能求出角B.(2)求出a+c=7,再由余弦定理得ac=12,由此能求出△ABC的面积.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,AD=1,M为CD的中点.如图将△ADM沿AM折起,使得平面ADM⊥平面ABCM.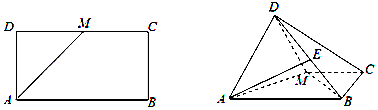
(Ⅰ)求证:BM⊥平面ADM;
(Ⅱ)若点E是线段DB上的中点,求三棱锥E﹣ABM的体积V1与四棱锥D﹣ABCM的体积V2之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图正方体ABCD﹣A1B1C1D1 , M,N分别为A1D1和AA1的中点,则下列说法中正确的个数为( ) 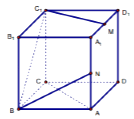
①C1M∥AC;
②BD1⊥AC;
③BC1与AC的所成角为60°;
④B1A1、C1M、BN三条直线交于一点.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=3x , g(x)=|x+a|﹣3,其中a∈R. (Ⅰ)若函数h(x)=f[g(x)]的图象关于直线x=2对称,求a的值;
(Ⅱ)给出函数y=g[f(x)]的零点个数,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个递增的等差数列{an}的前三项的和为﹣3,前三项的积为8.数列 ![]() 的前n项和为
的前n项和为 ![]() .
.
(1)求数列{an}的通项公式.
(2)求数列 ![]() 的通项公式.
的通项公式.
(3)是否存在一个等差数列{cn},使得等式 ![]() 对所有的正整数n都成立.若存在,求出所有满足条件的等差数列{cn}的通项公式,并求数列{bn}的前n项和Tn;若不存在,请说明理由.
对所有的正整数n都成立.若存在,求出所有满足条件的等差数列{cn}的通项公式,并求数列{bn}的前n项和Tn;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是( )
A.命题“若xy=0,则x=0”的否命题为“若xy≠0,则x≠0”
B.命题“?x∈R,x2﹣x﹣1≤0”的否定是“ ![]() ”
”
C.若p,q均为假命题,则p∧q为假命题
D.命题“?x∈[1,2],x2﹣a≤0”为真命题的一个充分不必要条件是a≥4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( ) 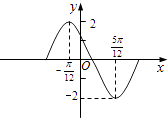
A.y=2sin(2x+ ![]() )
)
B.y=2sin(2x+ ![]() )
)
C.y=2sin( ![]() ﹣
﹣ ![]() )
)
D.y=2sin(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:函数f(x)=lg(ax2﹣x+ ![]() )的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
)的值域为R;命题q:3x﹣9x<a对一切实数x恒成立,如果命题“p且q”为假命题,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com