
【题目】已知数列![]() 的前
的前![]() 项积为
项积为![]() ,满足
,满足![]() . 数列
. 数列![]() 的首项为
的首项为![]() ,且满足
,且满足![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)记集合![]() ,若集合
,若集合![]() 的元素个数为
的元素个数为![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在正整数![]() 使得
使得![]() 成立?如果存在,请写出
成立?如果存在,请写出![]() 满足的条件,如果不存在,请说明理由.
满足的条件,如果不存在,请说明理由.
【答案】(1)![]() ,bn=2n;(2)
,bn=2n;(2)![]() ;(3)答案不唯一,见解析
;(3)答案不唯一,见解析
【解析】
(1)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,即可的
,即可的![]() 的通项公式,由
的通项公式,由![]() 可得
可得![]() ,即数列
,即数列![]() 是常数数列,即可求出
是常数数列,即可求出![]() 的通项公式;
的通项公式;
(2)参变分离,构造函数列![]() ,判断其增减性,即可求出
,判断其增减性,即可求出![]() 的取值范围;
的取值范围;
(3)假设存在,根据数列![]() 为等比数列,利用公式求出其前
为等比数列,利用公式求出其前![]() 项和,对
项和,对![]() 分类讨论.
分类讨论.
(1)因为![]() ,所以当
,所以当![]() 时,
时,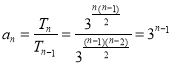
而当![]() 时,
时,![]() 适合上式,所以
适合上式,所以![]() ,因为
,因为![]() ,即
,即![]()
所以数列![]() 是常数数列,所以
是常数数列,所以![]() ,所以
,所以![]() .
.
(2)由(1)知,不等式![]() 即为
即为![]()
设![]()
因为![]()
![]()
而![]()
要使![]() 只有2解,则有
只有2解,则有![]()
(3)假设存在正整数![]() ,因为
,因为![]()
所以有![]() 若
若![]() ,则
,则![]() 不成立,
不成立,
所以![]() ,
,![]() ,若
,若![]() 为奇数,当
为奇数,当![]() 时,
时,![]() ,不成立,.
,不成立,.
当![]() 时,设
时,设![]() ,
,![]() , 则
, 则![]() .
.
若q为偶数,设![]() ,
,![]() ,则
,则![]() ,因为
,因为![]() ,所以
,所以![]() .
.
综上所述,当![]() 为大于1的奇数时,
为大于1的奇数时,![]() ,
,![]() ;
;
当q为偶数时,不存在.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 做斜率为
做斜率为![]() 的直线
的直线![]() ,椭圆
,椭圆![]() 与直线
与直线![]() 交于
交于![]() 两点,当直线
两点,当直线![]() 垂直于
垂直于![]() 轴时
轴时![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,在
变化时,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是以
是以![]() 为底的等腰三角形,若存在求出
为底的等腰三角形,若存在求出![]() 的取值范围,若不存在说明理由.
的取值范围,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某区在2019年教师招聘考试中,参加![]() 、
、![]() 、
、![]() 、
、![]() 四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
四个岗位的应聘人数、录用人数和录用比例(精确到1%)如下:
岗位 | 男性应聘人数 | 男性录用人数 | 男性录用比例 | 女性应聘人数 | 女性录用人数 | 女性录用比例 |
| 269 | 167 | 62% | 40 | 24 | 60% |
| 217 | 69 | 32% | 386 | 121 | 31% |
| 44 | 26 | 59% | 38 | 22 | 58% |
| 3 | 2 | 67% | 3 | 2 | 67% |
总计 | 533 | 264 | 50% | 467 | 169 | 36% |
(1)从表中所有应聘人员中随机抽取1人,试估计此人被录用的概率;
(2)将应聘![]() 岗位的男性教师记为
岗位的男性教师记为![]() ,女性教师记为
,女性教师记为![]() ,现从应聘
,现从应聘![]() 岗位的6人中随机抽取2人.
岗位的6人中随机抽取2人.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设![]() 为事件“抽取的2人性别不同”,求事件
为事件“抽取的2人性别不同”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() .
.
(1)证明:数列![]() 为等差数列;
为等差数列;
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,且对任意的正整数n,都有
,且对任意的正整数n,都有![]() ,求整数
,求整数![]() 的值;
的值;
(3)设数列![]() 满足
满足![]() ,若
,若![]() ,且存在正整数s,t,使得
,且存在正整数s,t,使得![]() 是整数,求
是整数,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有穷数列![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .若数列
.若数列![]() 中各项都是集合
中各项都是集合![]() 的元素,则称该数列为
的元素,则称该数列为![]() 数列.对于
数列.对于![]() 数列
数列![]() ,定义如下操作过程
,定义如下操作过程![]() :从
:从![]() 中任取两项
中任取两项![]() ,
,![]() ,将
,将![]() 的值添在
的值添在![]() 的最后,然后删除
的最后,然后删除![]() ,
,![]() ,这样得到一个
,这样得到一个![]() 项的新数列
项的新数列![]() (约定:一个数也视作数列).若
(约定:一个数也视作数列).若![]() 还是
还是![]() 数列,可继续实施操作过程
数列,可继续实施操作过程![]() ,得到的新数列记作
,得到的新数列记作![]() ,
,![]() ,如此经过
,如此经过![]() 次操作后得到的新数列记作
次操作后得到的新数列记作![]() .
.
(1)设![]() ,
,![]() ,
,![]() 请写出
请写出![]() 的所有可能的结果;
的所有可能的结果;
(2)求证:对于一个![]() 项的
项的![]() 数列
数列![]() 操作
操作![]() 总可以进行
总可以进行![]() 次;
次;
(3)设![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 求
求![]() 的可能结果,并说明理由.
的可能结果,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代计时器的发明时间不晚于战国时代(公元前476年~前222年),其中沙漏就是古代利用机械原理设计的一种计时装置,它由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道流到下部容器,如图,某沙漏由上、下两个圆锥容器组成,圆锥的底面圆的直径和高均为8 cm,细沙全部在上部时,其高度为圆锥高度的![]() (细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
(细管长度忽略不计).若细沙全部漏入下部后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,则此圆锥形沙堆的高为( )
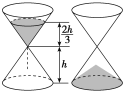
A.2 cmB.![]() cmC.
cmC.![]() cmD.
cmD.![]() cm
cm
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 、
、![]() 的定义域均为
的定义域均为![]() ,若对任意
,若对任意![]() ,且
,且![]() ,具有
,具有![]() ,则称函数
,则称函数![]() 为
为![]() 上的单调非减函数,给出以下命题:① 若
上的单调非减函数,给出以下命题:① 若![]() 关于点
关于点![]() 和直线
和直线![]() (
(![]() )对称,则
)对称,则![]() 为周期函数,且
为周期函数,且![]() 是
是![]() 的一个周期;② 若
的一个周期;② 若![]() 是周期函数,且关于直线
是周期函数,且关于直线![]() 对称,则
对称,则![]() 必关于无穷多条直线对称;③ 若
必关于无穷多条直线对称;③ 若![]() 是单调非减函数,且关于无穷多个点中心对称,则
是单调非减函数,且关于无穷多个点中心对称,则![]() 的图象是一条直线;④ 若
的图象是一条直线;④ 若![]() 是单调非减函数,且关于无穷多条平行于
是单调非减函数,且关于无穷多条平行于![]() 轴的直线对称,则
轴的直线对称,则![]() 是常值函数;以上命题中,所有真命题的序号是_________
是常值函数;以上命题中,所有真命题的序号是_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com