
| a |
| b |
| a |
| b |
|
| ||||
|
|
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| a |
| b |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
| a |
| b |
| a |
| b |
| e1 |
| e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| AB |
| AC |
| ||
|
|
| ||
|
|
| BC |
| ||
|
|
| ||
|
|
| 1 |
| 2 |
| A、等腰非等边三角形 |
| B、等边三角形 |
| C、三边均不相等的三角形 |
| D、直角三角形 |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省成都市高三第一次模拟文科数学卷 题型:填空题
已知非零向量 、
、 、
、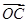 、
、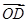 满足:
满足: =
= +
+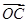 +g
+g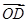 (,,gR),B、C、D为不共线三点,给出下列命题:
(,,gR),B、C、D为不共线三点,给出下列命题:
①若= ,=
,=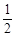 ,g,则A、B、C、D四点在同一平面上;
,g,则A、B、C、D四点在同一平面上;
②若==g, |+|
|+|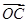 |+|
|+|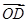 |=1,<
|=1,< ,
,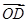 >=<
>=<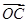 ,
,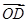 >=
>= ,<
,< ,
,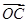 >=
>= ,则|
,则| |=2;
|=2;
③已知正项等差数列{an}(n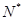 ,若a2,=a2009,g,且A、B、C三点共线,但O点不在直线BC上,则
,若a2,=a2009,g,且A、B、C三点共线,但O点不在直线BC上,则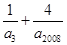 的最小值为10;
的最小值为10;
④若= ,=
,= ,g,则A、B、C三点共线且A分
,g,则A、B、C三点共线且A分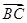 所成的比一定为4
所成的比一定为4
查看答案和解析>>
科目:高中数学 来源:2011年四川省成都市高考数学一模试卷(文科)(解析版) 题型:解答题
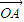 、
、 、
、 、
、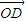 满足:
满足: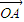 =α
=α Z+β
Z+β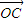 Z+γ
Z+γ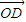 Z(α,β,γ∈R),B、C、D为不共线三点,给出下列命题:
Z(α,β,γ∈R),B、C、D为不共线三点,给出下列命题: ,β=
,β= ,γ=-1,则A、B、C、D四点在同一平面上;
,γ=-1,则A、B、C、D四点在同一平面上; Z|+|
Z|+| |+|
|+| |=1,<
|=1,< ,
, >=<
>=<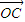 ,
, >=
>= ,<
,<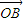 ,
,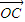 >=
>=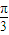 ,则|
,则| |=2;
|=2; 的最小值为10;
的最小值为10; ,β=-
,β=- Z,γ=0,则A、B、C三点共线且A分
Z,γ=0,则A、B、C三点共线且A分 所成的比λ一定为-4
所成的比λ一定为-4查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com