
����Ŀ���ס���������ѧ����Ϊѧϰ��Ҫ��������ѡ��һ̨�ʼDZ����ԣ����Ǿ�����A��B��C����Ʒ�Ƶ�����Ʒ��ѡ�������ʼDZ�������ij����ƽ̨�ļ۸����������������ʾ��
Ʒ�� | A | B | C | ||
�ͺ� | A��1 | A��2 | B��1 | B��2 | C��1 |
�۸�Ԫ�� | 6000 | 7500 | 10000 | 8000 | 4500 |
������̨�� | 1000 | 1000 | 200 | 800 | 3000 |
��������ѡ��ijƷ�ƵıʼDZ����Եĸ������Ʒ�Ƶ������������ȣ�����ѡ��BƷ�ƵıʼDZ����Եĸ��ʣ�
�������ס�������ѡ��ÿ���ͺŵıʼDZ����Եĸ��ʶ���ȣ�������ѡ�����ͺŲ���ͬ�����������˹���ıʼDZ����Եļ۸�֮�ʹ���15000Ԫ�ĸ��ʣ�
���𰸡�����![]() ����
����![]()
��������
�����������ȿ����ѡ��BƷ�Ƶĸ���Ϊp������ѡ��AƷ�ƺ�CƷ�Ƶĸ��ʷֱ�Ϊ2p��3p�����ɸ��ʺ�Ϊ1���ɵý⣻
���������оٷ��������ڹŵ���͵ļ��㹫ʽ��⼴��.
���������⣬A��B��C����Ʒ�Ƶ��������ֱ�Ϊ2000̨��1000̨��3000̨�������ı�Ϊ2��1��3��
���ѡ��BƷ�Ƶĸ���Ϊp������ѡ��AƷ�ƺ�CƷ�Ƶĸ��ʷֱ�Ϊ2p��3p��
��p+2p+3p��1�����p��![]() ��
��
���ѡ��BƷ�ƵıʼDZ����Եĸ���Ϊ![]() ��
��
���ס������˴����ʼDZ������и���ѡһ̨���۸���20��������ֱ�Ϊ��
��6000��7500������6000��10000������6000��8000������6000��4500������7500��6000����
��7500��10000������7500��8000������7500��4500������10000��6000������10000��7500����
��10000��8000������10000��4500������8000��6000������8000��7500������8000��10000����
��8000��4500������4500��6000������4500��7500������4500��10000������4500��80000����
�����������˹���ıʼDZ����Եļ۸�֮�ʹ���15000Ԫ��Ϊ�¼�M��
���¼�M�����������8�֣��ֱ�Ϊ��
��6000��10000������10000��6000������7500��10000������10000��7500����
��7500��8000������8000��7500������8000��10000������10000��8000����
���������˹���ıʼDZ����Եļ۸�֮�ʹ���15000Ԫ�ĸ��ʣ�![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й��Ŵ�����������������ָ:������������.ijУ��ѧ����Ԥ��������չ���������γ̽����,�����������ſ�����,ÿ��һ��,�ſ�������Ҫ��:����������������������,��������������Ҫ����,��������������γ̽�����IJ�ͬ�ſ�˳����( )
A.18��B.36��C.72��D.144��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() �У�
��![]() ��
��![]() ���DZ߳�Ϊ2�ĵȱ������Σ�
���DZ߳�Ϊ2�ĵȱ������Σ�![]() �Dz���
�Dz���![]() ���е㣬����
���е㣬����![]() ��ƽ����
��ƽ����![]() ��
��![]() ��ƽ��ֱ���
��ƽ��ֱ���![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() .
.
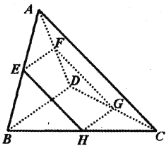
��1��֤�����ı���![]() Ϊ���Σ�
����
��2����ƽ��![]() ƽ��
ƽ��![]() ��������
��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ,
,![]()
![]() �ǵȱ������Σ�E��PA���е㣬
�ǵȱ������Σ�E��PA���е㣬![]() .
.

(1)��֤��![]() ��
��
(2)������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��˫����![]()
![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ����
����![]() ����б��Ϊ
����б��Ϊ![]() ��ֱ����
��ֱ����![]() ���˫���ߵ���֧�ֱ���
���˫���ߵ���֧�ֱ���![]() ���㣬����
���㣬����![]() ƽ���߶�
ƽ���߶�![]() �����˫���ߵ����������� ��
�����˫���ߵ����������� ��
A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ԲC��![]() �Ľ���Ϊ2
�Ľ���Ϊ2![]() �������϶������ߵ�б��Ϊ
�������϶������ߵ�б��Ϊ![]() ��
��
��������ԲC�ı����̣�
������P��m��0����Բx2+y2��1��һ������l����ԲC��M��N���㣬��|MN|��ֵ���ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ������
������![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() ����㣺��
����㣺��![]() �������
�������![]() ������
������![]() ������Сֵ�����ֵ����
������Сֵ�����ֵ����![]() �����ֵ�ǣ� ��
�����ֵ�ǣ� ��
A. 11B. 13C. 15D. 17
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ĵ���Ϊ���Σ�
�ĵ���Ϊ���Σ�![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣮
���е㣮
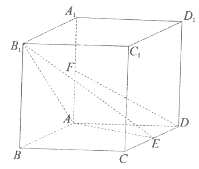
������֤��![]() ƽ��
ƽ��![]() ��
��
������֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() ��������ֱ��
��������ֱ��![]() ��
��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}���㣺a1+a2+a3+��+an=n-an����n=1��2��3������
������֤������{an-1}�ǵȱ����У�
������bn=��2-n����an-1����n=1��2��3�����������������n��N*������bn+![]() t��t2����ʵ��t��ȡֵ��Χ��
t��t2����ʵ��t��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com