
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,btanB+btanA=﹣2ctanB,且a=8,△ABC的面积为 ![]() ,则b+c的值为 .
,则b+c的值为 .
【答案】![]()
【解析】解:∵在△ABC中btanB+btanA=﹣2ctanB, ∴由正弦定理可得sinB(tanA+tanB)=﹣2sinCtanB,
∴sinB(tanA+tanB)=﹣2sinC ![]() ,
,
∴cosB(tanA+tanB)=﹣2sinC,
∴cosB( ![]() +
+ ![]() )=﹣2sinC,
)=﹣2sinC,
∴cosB ![]() =﹣2sinC,
=﹣2sinC,
∴cosB ![]() =
= ![]() =﹣2sinC,
=﹣2sinC,
解得cosA=﹣ ![]() ,A=
,A= ![]() ;
;
∵a=8,由余弦定理可得:64=b2+c2+bc=(b+c)2﹣bc,①
∵△ABC的面积为 ![]() =
= ![]() bcsinA=
bcsinA= ![]() bc,可得:bc=16,②
bc,可得:bc=16,②
∴联立①②可得:b+c=4 ![]() .
.
所以答案是:4 ![]() .
.
【考点精析】关于本题考查的正弦定理的定义,需要了解正弦定理:![]() 才能得出正确答案.
才能得出正确答案.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图,某市在海岛A上建了一水产养殖中心.在海岸线l上有相距70公里的B、C两个小镇,并且AB=30公里,AC=80公里,已知B镇在养殖中心工作的员工有3百人,C镇在养殖中心工作的员工有5百人.现欲在BC之间建一个码头D,运送来自两镇的员工到养殖中心工作,又知水路运输与陆路运输每百人每公里运输成本之比为1:2. 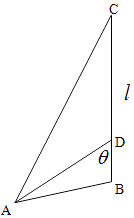
(1)求sin∠ABC的大小;
(2)设∠ADB=θ,试确定θ的大小,使得运输总成本最少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司过去五个月的广告费支出![]() 与销售额
与销售额![]() (单位:万元)之间有下列对应数据:
(单位:万元)之间有下列对应数据:
| 2 | 4 | 5 | 6 | 8 |
|
| 40 | 60 | 50 | 70 |
工作人员不慎将表格中![]() 的第一个数据丢失.已知
的第一个数据丢失.已知![]() 对
对![]() 呈线性相关关系,且回归方程为
呈线性相关关系,且回归方程为![]() ,则下列说法:①销售额
,则下列说法:①销售额![]() 与广告费支出
与广告费支出![]() 正相关;②丢失的数据(表中
正相关;②丢失的数据(表中![]() 处)为30;③该公司广告费支出每增加1万元,销售额一定增加
处)为30;③该公司广告费支出每增加1万元,销售额一定增加![]() 万元;④若该公司下月广告投入8万元,则销售
万元;④若该公司下月广告投入8万元,则销售
额为70万元.其中,正确说法有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】极坐标系中椭圆C的方程为ρ2= ![]() ,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
,以极点为原点,极轴为x轴非负半轴,建立平面直角坐标系,且两坐标系取相同的单位长度.
(1)若椭圆上任一点坐标为P(x,y),求 ![]() 的取值范围;
的取值范围;
(2)若椭圆的两条弦AB,CD交于点Q,且直线AB与CD的倾斜角互补,求证:|QA||QB|=|QC||QD|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( ) 
A.![]() (a>0,b>0)
(a>0,b>0)
B.a2+b2≥2ab(a>0,b>0)
C.![]() (a>0,b>0)
(a>0,b>0)
D.![]() (a>0,b>0)
(a>0,b>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED为矩形,平面BFED⊥平面ABCD,BF=1.
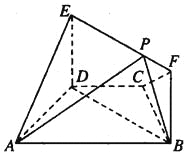
(1)求证:AD⊥平面BFED;
(2)已知点P在线段EF上,![]() =2.求三棱锥E-APD的体积.
=2.求三棱锥E-APD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
的焦点为F,过F作平行于x轴的直线交抛物线于A,B两点(A在B的左侧),若△AOB的面积为2.
(1)求抛物线C的方程;
(2)设P是抛物线C的准线上一点,Q是抛物线上的一点,若PF⊥QF,求证:直线PQ与抛物线相切.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com