
����Ŀ��Ϊ��ʵ����ɫ��չ�������˷���Դ��ij�������ƻ��Ծ����õ���ý����շѵķ���.Ϊ�ˣ���ز����ڸ������������![]() ���������·ݵ��õ�������λ��
���������·ݵ��õ�������λ��![]() ���ͼ�ͥ���루��λ����Ԫ�������˽�������м�ͥ�õ��������.
���ͼ�ͥ���루��λ����Ԫ�������˽�������м�ͥ�õ��������.
�õ����������£�
![]() .
.
��Ӧ�ļ�ͥ�����������£�
![]()
![]() .
.
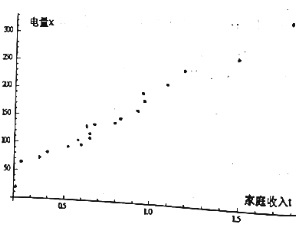
���������ݹ��ҷ���ί��ָʾ�����мƻ�ʵʩ![]() ���ݵ����ʹ
���ݵ����ʹ![]() ���û��ڵ�һ�������Ϊ
���û��ڵ�һ�������Ϊ![]() Ԫ/
Ԫ/![]() ��
��![]() ���û��ڵڶ��������Ϊ
���û��ڵڶ��������Ϊ![]() Ԫ/
Ԫ/![]() ��
��![]() ���û��ڵ����������Ϊ
���û��ڵ����������Ϊ![]() Ԫ/
Ԫ/![]() ������������õ����
������������õ����![]() ���õ���
���õ���![]() ��ĺ�����ϵ��
��ĺ�����ϵ��
�������Լ�ͥ����![]() Ϊ������������
Ϊ������������![]() Ϊ����������ɢ��ͼ����ͼ������
Ϊ����������ɢ��ͼ����ͼ������![]() ����
����![]() �Ļع�ֱ�߷��̣��ع�ֱ�߷��̵�ϵ���������뱣��������.
�Ļع�ֱ�߷��̣��ع�ֱ�߷��̵�ϵ���������뱣��������.
������С���ҵ�������![]() Ԫ����������ϵ������С������֧����Ѷ���Ԫ��
Ԫ����������ϵ������С������֧����Ѷ���Ԫ��
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .
.
�ο���ʽ��һ���������![]() ��
��![]() ������
������![]() �Ļع�ֱ�߷���
�Ļع�ֱ�߷���![]() ��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ
��б�ʺͽؾ����С���˷����Ʒֱ�Ϊ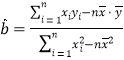 ��
��![]() ������
������![]() ��
��![]() Ϊ������ֵ.
Ϊ������ֵ.
���𰸡�(1)  .
.
(2) ![]() .
.
(3) 72.8Ԫ.
������������������![]()
![]() ��
��![]() ���õ��������еõ���һ�����ٽ�ֵΪ��15����������180���ڶ������ٽ�ֵΪ��19����������260���Ӷ��ɵþ����õ����
���õ��������еõ���һ�����ٽ�ֵΪ��15����������180���ڶ������ٽ�ֵΪ��19����������260���Ӷ��ɵþ����õ����![]() ���õ���
���õ���![]() ��ĺ�����ϵ��
��ĺ�����ϵ��
�����������⣬![]() ��
��![]() �����빫ʽ���㼴����
�����빫ʽ���㼴����
��������ع�ֱ�߷��̼���.
�������I����Ϊ![]() ��
��
���Դ��õ��������еõ���һ�����ٽ�ֵΪ��15����������180��
�ڶ������ٽ�ֵΪ��19����������260����ˣ�

���ԣ�
��II������![]() ��
��
![]() ��
��
 ��
��
����![]() ��
��
�Ӷ��ع�ֱ�߷���Ϊ![]() ��
��
����![]() ʱ��
ʱ��![]() ��
��
![]() �����ԣ�С������֧�����72.8Ԫ��
�����ԣ�С������֧�����72.8Ԫ��
��ܰ��ʾ������ѧ���ֹ����㣬�������������������ļ�������������ʦ����۷֡�����ڣ�����0���ڣ������������ڡ�3����������0�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx+1��
����֤������x��0ʱ��f��x����x��
������ ![]() ����g��x����0��x��0���������ʵ��a��ȡֵ��Χ��
����g��x����0��x��0���������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=alnx+x2+bx��aΪʵ��������
��1����a=��2��b=��3����f��x���ĵ������䣻
��2����b=0����a����2e2 �� ����f��x����[1��e]�ϵ���Сֵ����Ӧ��xֵ��
��3����b=0��������x��[1��e]��ʹ��f��x���ܣ�a+2��x��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�Ӹ��������������ȡn��ѧ�������ߣ��������������õ���Ƶ�ʷֲ��������ʾ��
��� | ���� | Ƶ�� | Ƶ�� |
��1�� |
| 5 | 0.05 |
��2�� |
| a | 0.35 |
��3�� |
| 30 | b |
��4�� |
| 20 | 0.20 |
��5�� |
| 10 | 0.10 |
�ϼ� | n | 1.00 | |
��1�����Ƶ�ʷֲ�����![]() ��ֵ�����������Ƶ�ʷֲ�ֱ��ͼ��
��ֵ�����������Ƶ�ʷֲ�ֱ��ͼ��
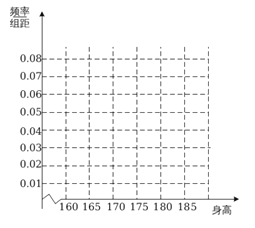
��2��Ϊ���ܶ�ѧ������������һ���˽⣬��У�����ڵ�1��4��5�����÷ֲ����ȡ7��ѧ�����в�ͬ��Ŀ�����ܲ��ԣ�������7��ѧ���������ȡ2��ѧ�������������ϲ��ԣ����4����������һ��ѧ�������еĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����գ�x��= ![]() ��a��0
��a��0
��1��������f��x��=lnx+�գ�x�����ڣ�1��2����ֻ��һ����ֵ�㣬��a��ȡֵ��Χ��
��2����g��x��=|lnx|+�գ�x�����Ҷ�����x1 �� x2�ʣ�0��2]����x1��x2 �� ���� ![]() ����1����a��ȡֵ��Χ��
����1����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����ô���н����д�����ǣ� ��
����ô���н����д�����ǣ� ��
A. ��![]() ��
��![]() �ļ�Сֵ�㣬��
�ļ�Сֵ�㣬��![]() ������
������![]() �ϵ����ݼ�
�ϵ����ݼ�
B. ![]() ��ʹ
��ʹ![]()
C. ����![]() ��ͼ����������ĶԳ�ͼ��
��ͼ����������ĶԳ�ͼ��
D. ��![]() ��
��![]() �ļ�ֵ�㣬��
�ļ�ֵ�㣬��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Բ ![]() +
+ ![]() =1��a��b��0������ΪF���Ҷ���ΪA��������Ϊ
=1��a��b��0������ΪF���Ҷ���ΪA��������Ϊ ![]() ����֪A��������y2=2px��p��0���Ľ��㣬F�������ߵ���l�ľ���Ϊ
����֪A��������y2=2px��p��0���Ľ��㣬F�������ߵ���l�ľ���Ϊ ![]() ��
��
��������Բ�ķ��̺������ߵķ��̣�
������l������P��Q����x��Գƣ�ֱ��AP����Բ�ཻ�ڵ�B��B����A����ֱ��BQ��x���ཻ�ڵ�D������APD�����Ϊ ![]() ����ֱ��AP�ķ��̣�
����ֱ��AP�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ������
������![]() ����Բ����ֱ��
����Բ����ֱ��![]() ��
��![]() ��.
��.
��1����Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ����Բ
��ֱ����Բ![]() ����
����![]() ���㣬����ֱ��
���㣬����ֱ��![]() ���Ƿ���ڶ���
���Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() ������������ڣ��������
������������ڣ��������![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f��x��=sin����x�� ![]() ��+sin����x��
��+sin����x�� ![]() ��������0���أ�3����֪f��
��������0���أ�3����֪f�� ![]() ��=0����12�֣�
��=0����12�֣�
������أ�
��������y=f��x����ͼ���ϸ���ĺ������쳤Ϊԭ����2���������겻�䣩���ٽ��õ���ͼ������ƽ�� ![]() ����λ���õ�����y=g��x����ͼ����g��x����[��
����λ���õ�����y=g��x����ͼ����g��x����[�� ![]() ��
�� ![]() ]�ϵ���Сֵ��
]�ϵ���Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com