B
分析:A画出正态分布N(0,σ
2)的密度函数的图象,由图象的对称性可得结果;B、判断命题p和q是否正确,然后根据交集的定义进行判断;C、根据回归直线方程的x的系数是-2.5,得到变量x增加一个单位时,函数值要平均增加-2.5个单位,即可求解;D、注意斜率不存在的情况即可判定正误;
解答:A、由随机变量ξ服从正态分布N(0,σ
2)可知正态密度曲线关于y轴对称,

而P(-2≤x≤2)=0.4,
则P(ξ>2)=

(1-P(-2≤x≤2))=0.3,故A错.
B、命题p:?x∈R,使tanx=1,可以取x=45°得tan45°=1,故命题p正确;
命题q:?x,x
2-x+1>0,令f(x)=x
2-x+1,可得△=(-1)
2-4=-3<0,图象开口向上,与x轴无交点,∴:?x∈R,x
2-x+1>0,恒成立,
∴命题q为真命题,则-q为假命题,∴“p∧-q”是假命题,故B正确;
C、回归方程y=2-2.5x,变量x增加一个单位时,
变量y平均变化[2-2.5(x+1)]-(2-2.5x)=-2.5
∴变量y平均减少2.5个单位,故C错误;
D、已知直线l
1:ax+3y-1=0,l
2:x+by+1=0,则l
1⊥l
2的
充要条件是

=-3或a=0且b=0,所以D不正确.
故选B;
点评:本题考查线性回归方程和两条直线垂直的判定,考查线性回归方程系数的意义,考查变量y增加或减少的是一个平均值,注意题目的叙述,还有充分必要条件的定义,是一道综合题;

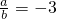

 (1-P(-2≤x≤2))=0.3,故A错.
(1-P(-2≤x≤2))=0.3,故A错. =-3或a=0且b=0,所以D不正确.
=-3或a=0且b=0,所以D不正确.
