
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位:t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量X∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率),求T的数学期望.
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:解答题
已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.
(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
参加市数学调研抽测的某校高三学生成绩分析的茎叶图和频率分布直方图均受到不同程度的破坏,但可见部分信息如下,据此解答如下问题:
(1)求参加数学抽测的人数 、抽测成绩的中位数及分数分别在
、抽测成绩的中位数及分数分别在 ,
, 内的人数;
内的人数;
(2)若从分数在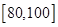 内的学生中任选两人进行调研谈话,求恰好有一人分数在
内的学生中任选两人进行调研谈话,求恰好有一人分数在 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校高一年级 名学生参加数学竞赛,成绩全部在
名学生参加数学竞赛,成绩全部在 分至
分至 分之间,现将成绩分成以下
分之间,现将成绩分成以下 段:
段:
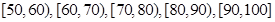 ,据此绘制了如图所示的频率分布直方图.
,据此绘制了如图所示的频率分布直方图. 
(1)求成绩在区间 的频率;
的频率;
(2)从成绩大于等于 分的学生中随机选
分的学生中随机选 名学生,其中成绩在
名学生,其中成绩在 内的学生人数为
内的学生人数为 ,求
,求 的分布列与均值.
的分布列与均值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种报纸,进货商当天以每份1元从报社购进,以每份2元售出.若当天卖不完,剩余报纸报社以每份0.5元的价格回收.根据市场统计,得到这个季节的日销售量X(单位:份)的频率分布直方图(如图所示),将频率视为概率.
(1)求频率分布直方图中a的值;
(2)若进货量为n(单位:份),当n≥X时,求利润Y的表达式;
(3)若当天进货量n=400,求利润Y的分布列和数学期望E(Y)(统计方法中,同一组数据常用该组区间的中点值作为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
经销商经销某种农产品,在一个销售季度内,每售出 t该产品获利润
t该产品获利润 元,未售出的产品,每
元,未售出的产品,每 t亏损
t亏损 元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了
元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示。经销商为下一个销售季度购进了 t该农产品,以
t该农产品,以 (单位:t,
(单位:t, )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, (单位:元)表示下一个销售季度内销商该农产品的利润。
(单位:元)表示下一个销售季度内销商该农产品的利润。
(1)将 表示为
表示为 的函数;(2)根据直方图估计利润
的函数;(2)根据直方图估计利润 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对某校高一年级学生参加社区服务次数进行统计,随机抽取了M名学生作为样本,得到这M名学生参加社区服务的次数,根据数据作出了频数的统计如下:
| 分组 | 频数 | 频率 |
| [10,15) | 9 | 0.45 |
| [15,20) | 5 | n |
| [20,25) | m | r |
| [25,30) | 2 | 0.1 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某校有教职工 人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
人,对他们进行年龄状况和受教育情况(只有本科和研究生两类)的调查,其结果如图:
(Ⅰ)随机抽取一人,是35岁以下的概率为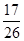 ,求
,求 的值;
的值;
(Ⅱ)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班样本的方差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com