
【题目】如图所示,有两条相交成60°角的直线![]() ,交点为
,交点为![]() .甲、乙分别在
.甲、乙分别在![]() 上,起初甲离
上,起初甲离![]() 点
点![]() ,乙离
,乙离![]() 点
点![]() ,后来甲沿
,后来甲沿![]() 的方向,乙沿
的方向,乙沿![]() 的方向,同时以
的方向,同时以![]() 的速度步行.求:
的速度步行.求:

(1)起初两人的距离是多少?
(2)![]() 后两人的距离是多少?
后两人的距离是多少?
(3)什么时候两人的距离最短?
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (c为常数),且f(1)=0.
(c为常数),且f(1)=0.
(1)求c的值;
(2)证明函数f(x)在[0,2]上是单调递增函数;
(3)已知函数g(x)=f(ex),判断函数g(x)的奇偶性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014福建)在下列向量组中,可以把向量 ![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0), ![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2), ![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5), ![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图. 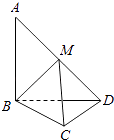
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E: ![]() ﹣
﹣ ![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x. 
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在 R 上的奇函数 f (x) ,设其导函数为 f x ,当 x ,0时,恒有xf x f x 0 ,令 F x xf x,则满足 F(3) F 2x 1 的实数 x 的取值范围是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明在10场篮球比赛中的投篮情况统计如下(假设各场比赛相互独立);
场次 | 投篮次数 | 命中次数 | 场次 | 投篮次数 | 命中次数 |
主场1 | 22 | 12 | 客场1 | 18 | 8 |
主场2 | 15 | 12 | 客场2 | 13 | 12 |
主场3 | 12 | 8 | 客场3 | 21 | 7 |
主场4 | 23 | 8 | 客场4 | 18 | 15 |
主场5 | 24 | 20 | 客场5 | 25 | 12 |
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过0.6的概率;
(2)从上述比赛中随机选择一个主场和一个客场,求李明的投篮命中率一场超过0.6,一场不超过0.6的概率;
(3)记 ![]() 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与
是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X为李明在这场比赛中的命中次数,比较EX与 ![]() 的大小(只需写出结论).
的大小(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com