
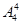 =24种对应方法,
=24种对应方法,

科目:高中数学 来源: 题型:
某初级中学有学生![]() 人,其中初一年级
人,其中初一年级![]() 人,初二、三年级各有
人,初二、三年级各有![]() 人,现要利用抽样方法取
人,现要利用抽样方法取![]() 人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按初一、二、三年级依次统一编号为
人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按初一、二、三年级依次统一编号为![]() ;使用系统抽样时,将学生统一随机编号为
;使用系统抽样时,将学生统一随机编号为![]() ,并将整个编号依次分为
,并将整个编号依次分为![]() 段.如果抽得号码(10个)有下列四种情况:
段.如果抽得号码(10个)有下列四种情况:
①7,34,61,88,115,142,169,196, 223, 250;
②5,9,100,107,111,121,180,195, 200,265;
③11,38,65,92,119,146,173,200, 227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( ▲ )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
查看答案和解析>>
科目:高中数学 来源: 题型:
某初级中学有学生![]() 人,其中初一年级
人,其中初一年级![]() 人,初二、三年级各有
人,初二、三年级各有![]() 人,现要利用抽样方法取
人,现要利用抽样方法取![]() 人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按初一、二、三年级依次统一编号为
人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按初一、二、三年级依次统一编号为![]() ;使用系统抽样时,将学生统一随机编号为
;使用系统抽样时,将学生统一随机编号为![]() ,并将整个编号依次分为
,并将整个编号依次分为![]() 段.如果抽得号码(10个)有下列四种情况:
段.如果抽得号码(10个)有下列四种情况:
①7,34,61,88,115,142,169,196, 223, 250;
②5,9,100,107,111,121,180,195, 200,265;
③11,38,65,92,119,146,173,200, 227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( ▲ )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com