
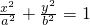 (a>b>0)的左、右焦点分别为F1、F2,若经过点F1且与x轴、y轴不平行的直线与该椭圆交于A、B两点,则下列结论错误的是________(把你认为错误的结论序号都写上).
(a>b>0)的左、右焦点分别为F1、F2,若经过点F1且与x轴、y轴不平行的直线与该椭圆交于A、B两点,则下列结论错误的是________(把你认为错误的结论序号都写上).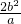 ,2a);
,2a);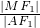 ;
;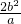 且最大值为2a,由此可得①是错误的;根据圆与圆的位置关系判断,结合椭圆的定义和三角形中位线定理,可得以AF1为直径的圆与椭圆长轴为直径的圆相切,故②正确;根据三角形内角平分线定理,结合比例的性质和椭圆离心率公式,可得③正确;根据椭圆的几何性质求得△ABF2的面积最大值不是a,得④错误.由此可得本题的正确答案.
且最大值为2a,由此可得①是错误的;根据圆与圆的位置关系判断,结合椭圆的定义和三角形中位线定理,可得以AF1为直径的圆与椭圆长轴为直径的圆相切,故②正确;根据三角形内角平分线定理,结合比例的性质和椭圆离心率公式,可得③正确;根据椭圆的几何性质求得△ABF2的面积最大值不是a,得④错误.由此可得本题的正确答案.
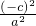 +
+ =1,解之得n=
=1,解之得n= (舍负)
(舍负)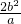 ,而当AB与椭圆的长轴重合时,|AB|最大值为2a,
,而当AB与椭圆的长轴重合时,|AB|最大值为2a,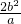 ,2a],故①是错误的;
,2a],故①是错误的; |AF2|=a-|NF1|,
|AF2|=a-|NF1|, =
= =
= =
= =
=
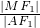 ,故③正确;
,故③正确; ×
×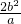 ×2c=
×2c=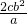 ≠a
≠a

科目:高中数学 来源:2010-2011学年河北冀州中学高二年级下学期第三次月考题(文) 题型:解答题
已知椭圆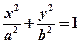 (a>b>0)的离心率e=
(a>b>0)的离心率e=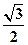 ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l与椭圆相交于不同的两点A、B,已知点A的坐标为
(i)若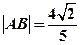 ,求直线l的倾斜角;
,求直线l的倾斜角;
(ii)若点Q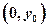 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且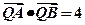 .求
.求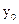 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷14(理科)(解析版) 题型:解答题
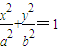 (a>b>0)的右焦点为F2(3,0),离心率为
(a>b>0)的右焦点为F2(3,0),离心率为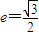 .
.查看答案和解析>>
科目:高中数学 来源:2011年湖北省天门市高考数学模拟试卷3(文科)(解析版) 题型:解答题
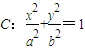 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆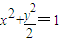 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.查看答案和解析>>
科目:高中数学 来源:2011年广东省广州市华侨中学高三一轮复习检测数学试卷(理科)(解析版) 题型:解答题
 (a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 .
(a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 .查看答案和解析>>
科目:高中数学 来源:2010年河北省邯郸市高二上学期期末考试数学理卷 题型:解答题
(本小题满分 分)
分)
(普通高中)已知椭圆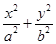 (a>b>0)的离心率
(a>b>0)的离心率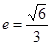 ,焦距是函数
,焦距是函数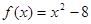 的零点.
的零点.
(1)求椭圆的方程;
(2)若直线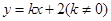 与椭圆交于
与椭圆交于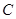 、
、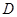 两点,
两点,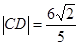 ,求k的值.
,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com