
【题目】函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示. 
(1)求f(x)的解析式,并求函数f(x)在[﹣ ![]() ,
, ![]() ]上的值域;
]上的值域;
(2)在△ABC中,AB=3,AC=2,f(A)=1,求sin2B.
【答案】
(1)解:根据图形知,函数的周期T= ![]() (
( ![]() ﹣
﹣ ![]() )=π,
)=π,
所以ω= ![]() =
= ![]() =2;
=2;
又y=2sin(2x+φ)的图象经过( ![]() ,2),
,2),
所以2× ![]() +φ=2kπ+
+φ=2kπ+ ![]() ,k∈Z;
,k∈Z;
所以φ=2kπ+ ![]() ,k∈Z;
,k∈Z;
又,φ∈(0,π),
所以φ= ![]() .f(x)的解析式:f(x)=2sin(2x+
.f(x)的解析式:f(x)=2sin(2x+ ![]() ).
).
x∈[﹣ ![]() ,
, ![]() ],可得:2x+
],可得:2x+ ![]() ∈[0,
∈[0, ![]() ],
],
sin(2x+ ![]() )∈[0,1]
)∈[0,1]
函数f(x)在[﹣ ![]() ,
, ![]() ]上的值域:[0,2]
]上的值域:[0,2]
(2)解:f(A)=2sin(2A+ ![]() )=1.∴sin(2A+
)=1.∴sin(2A+ ![]() )=
)= ![]() ,
,
∵2A+ ![]() ∈(
∈( ![]() ,
, ![]() ),∴2A+
),∴2A+ ![]() =
= ![]() .
.
在三角形ABC中,由余弦定理可得:BC2=9+4 ![]() ∴BC=
∴BC= ![]() .
.
由正弦定理可得: ![]() ,
,
故sinB= ![]() ,又AC<AB,∴∠B为锐角,∴cosB=
,又AC<AB,∴∠B为锐角,∴cosB= ![]() ,
,
∴sin2B=2sinBcosB= ![]() =
= ![]()
【解析】(1)根据图形,求出正确与ω的值,再由函数y的图象经过点( ![]() ,2),结合φ∈(0,π),即可求出φ的值.得到函数的解析式,求出自变量的范围,相位的范围,然后求解函数值域.(2)利用函数的解析式求出A,利用余弦定理以及正弦定理求解即可.
,2),结合φ∈(0,π),即可求出φ的值.得到函数的解析式,求出自变量的范围,相位的范围,然后求解函数值域.(2)利用函数的解析式求出A,利用余弦定理以及正弦定理求解即可.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+(a+1)x+a2(a∈R),若f(x)能表示成一个奇函数g(x)和一个偶函数h(x)的和.
(1)求g(x)和h(x)的解析式;
(2)若f(x)和g(x)在区间(-∞,(a+1)2]上都是减函数,求f(1)的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆O是△ABC的外接圆,∠BAC的平分线交BC于点F,D是AF的延长线与⊙O的交点,AC的延线与⊙O的切线DE交于点E. 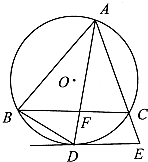
(1)求证: ![]() =
= ![]()
(2)若BD=3 ![]() ,EC=2,CA=6,求BF的值.
,EC=2,CA=6,求BF的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积= ![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为 ![]() ,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( )
,半径等于4米的弧田,按照上述经验公式计算所得弧田面积约是( ) 
A.6平方米
B.9平方米
C.12平方米
D.15平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an+1+an=104n﹣1(n∈N*),数列{bn}的前n项和为Sn , 且bn=log2an .
(1)求bn , Sn;
(2)设cn= ![]() ,证明:
,证明: ![]() +
+ ![]() +…+
+…+ ![]() <
< ![]() Sn+1(n∈N*).
Sn+1(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且满足不等式22a+1>25a﹣2.
(1)求实数a的取值范围;
(2)求不等式loga(3x+1)<loga(7﹣5x);
(3)若函数y=loga(2x﹣1)在区间[1,3]有最小值为﹣2,求实数a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com