
【题目】已知椭圆![]() :
:![]() (
(![]() ),右焦点
),右焦点![]() ,点
,点![]() 在椭圆上;
在椭圆上;
(1)求椭圆C的标准方程;
(2)是否存在过原点的直线l与椭圆C交于A、B两点,且![]() ?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
?若存在,请求出所有符合要求的直线;若不存在,请说明理由.
科目:高中数学 来源: 题型:
【题目】每年六、七月份,我国长江中下游地区进入持续25天左右的梅雨季节,如图是江南某地区![]() 年10年间梅雨季节的降雨量
年10年间梅雨季节的降雨量![]() 单位:
单位:![]() 的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
的频率分布直方图,试用样本频率估计总体概率,解答下列问题:
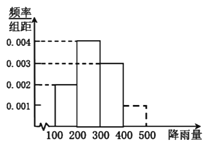
![]() 假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
假设每年的梅雨季节天气相互独立,求该地区未来三年里至少有两年梅雨季节的降雨量超过350mm的概率.
![]() 老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元
老李在该地区承包了20亩土地种植杨梅,他过去种植的甲品种杨梅,平均每年的总利润为28万元![]() 而乙品种杨梅的亩产量
而乙品种杨梅的亩产量![]() 亩
亩![]() 与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为
与降雨量之间的关系如下面统计表所示,又知乙品种杨梅的单位利润为![]() 元
元![]() ,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润
,请你帮助老李分析,他来年应该种植哪个品种的杨梅可以使总利润![]() 万元
万元![]() 的期望更大?并说明理由.
的期望更大?并说明理由.
降雨量 |
|
|
|
|
亩产量 | 500 | 700 | 600 | 400 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自由购是一种通过自助结算购物的形式.某大型超市为调查顾客自由购的使用情况,随机抽取了100人,调查结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(1)现随机抽取1名顾客,试估计该顾客年龄在[30,50)且未使用自由购的概率;
(2)从被抽取的年龄在[50,70]使用的自由购顾客中,随机抽取2人进一步了解情况,求这2人年龄都在[50,60)的概率;
(3)为鼓励顾客使用自由购,该超市拟对使用自由购顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,函数
,函数![]() .
.
(1)求实数![]() 的值,使得
的值,使得![]() 为奇函数;
为奇函数;
(2)若关于![]() 的方程
的方程![]() 有两个不同实数解,求
有两个不同实数解,求![]() 的取值范围;
的取值范围;
(3)若关于![]() 的不等式
的不等式![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人上午7时乘船出发,以匀速![]() 海里/小时
海里/小时![]() 从
从![]() 港前往相距50海里的
港前往相距50海里的![]() 港,然后乘汽车以匀速
港,然后乘汽车以匀速![]() 千米/小时(
千米/小时(![]() )自
)自![]() 港前往相距
港前往相距![]() 千米的
千米的![]() 市,计划当天下午4到9时到达
市,计划当天下午4到9时到达![]() 市.设乘船和汽车的所要的时间分别为
市.设乘船和汽车的所要的时间分别为![]() 、
、![]() 小时,如果所需要的经费
小时,如果所需要的经费![]() (单位:元)
(单位:元)

(1)试用含有![]() 、
、![]() 的代数式表示
的代数式表示![]() ;
;
(2)要使得所需经费![]() 最少,求
最少,求![]() 和
和![]() 的值,并求出此时的费用.
的值,并求出此时的费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,直线
,直线![]() 和
和![]() 相交于点
相交于点![]() ,且
,且![]() 和
和![]() 的斜率之差是1.
的斜率之差是1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过轨迹![]() 上的点
上的点![]() ,
,![]() ,作圆
,作圆![]() :
:![]() 的两条切线,分别交
的两条切线,分别交![]() 轴于点
轴于点![]() ,
,![]() .当
.当![]() 的面积最小时,求
的面积最小时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥S-ABCD的底面为正方形,![]()
![]() ,AC与BD交于E,M,N分别为SD,SA的中点,
,AC与BD交于E,M,N分别为SD,SA的中点,![]() .
.
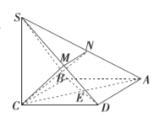
(1)求证:平面![]() 平面SBD;
平面SBD;
(2)求直线BD与平面CMN所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2013年发放汽车牌照12万张,其中燃油型汽车牌照10万张,电动型汽车2万张,为了节能减排和控制总量,从2013年开始,每年电动型汽车牌照按50%增长,而燃油型汽车牌照每一年比上一年减少0.5万张,同时规定一旦某年发放的牌照超过15万张,以后每一年发放的电动车的牌照的数量维持在这一年的水平不变.
(1)记2013年为第一年,每年发放的燃油型汽车牌照数量构成数列![]() ,每年发放电动型汽车牌照数为构成数列
,每年发放电动型汽车牌照数为构成数列![]() ,完成下列表格,并写出这两个数列的通项公式;
,完成下列表格,并写出这两个数列的通项公式;
(2)从2013年算起,累计各年发放的牌照数,哪一年开始超过200万张?
|
|
|
| |
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com