
【题目】已知命题p:x∈R,ex-mx=0,q:x∈R,x2-2mx+1≥0,若p∨(![]() q)为假命题,则实数m的取值范围是________.
q)为假命题,则实数m的取值范围是________.
【答案】![]() .
.
【解析】
根据复合函数的真假关系,确定命题p,q的真假,利用函数的性质分别求出对应的取值范围即可得到结论.
若p∨(q)为假命题,则p,q都为假命题,即p是假命题,q是真命题,
由ex﹣mx=0得m=![]() ,
,
设f(x)=![]() ,则f′(x)=
,则f′(x)=![]() =
=![]() ,
,
当x>1时,f′(x)>0,此时函数单调递增,
当0<x<1时,f′(x)<0,此时函数单调递递减,
当x<0时,f′(x)<0,此时函数单调递递减,
∴当x=1时,f(x)=![]() 取得极小值f(1)=e,
取得极小值f(1)=e,
∴函数f(x)=![]() 的值域为(﹣∞,0)∪[e,+∞),
的值域为(﹣∞,0)∪[e,+∞),
∴若p是假命题,则0≤m<e;
命题q为真命题时,有Δ=4m2-4≤0,则-1≤m≤1.
所以当p∨(![]() q)为假命题时,m的取值范围是[0,1].
q)为假命题时,m的取值范围是[0,1].
故答案为:![]()


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】f(x)是定义在(0,+∞)上的单调增函数,满足f(xy)=f(x)+f(y),f(3)=1,当f(x)+f(x-8)≤2时,x的取值范围是( )
A. (8,+∞) B. (8,9] C. [8,9] D. (0,8)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|x2-4x+3|.
(1)作出函数f(x)的图象;
(2)求函数f(x)的单调区间,并指出其单调性;
(3)求集合M={m|使方程f(x)=m有四个不相等的实根}.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用![]() ,
,![]() 分别表示乌龟和兔子所行的路程,
分别表示乌龟和兔子所行的路程,![]() 为时间,则与故事情节相吻合的是( )
为时间,则与故事情节相吻合的是( )
A.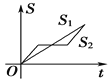 B.
B.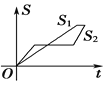 C.
C.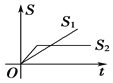 D.
D.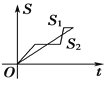
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 部分图象如图所示.
部分图象如图所示. 
(Ⅰ)求φ值及图中x0的值;
(Ⅱ)在△ABC中,A,B,C的对边分别为a,b,c,已知 ![]() ,f(C)=﹣2,sinB=2sinA,求a的值.
,f(C)=﹣2,sinB=2sinA,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com