
【题目】在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点.
的中点.
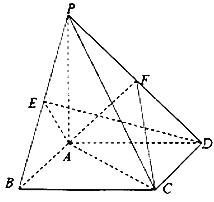
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求三棱锥![]() 的体积;
的体积;
(Ⅲ)求证:平面![]() 平面
平面![]() .
.
科目:高中数学 来源: 题型:
【题目】函数f(x)=loga(3﹣ax)(a>0,a≠1)
(1)当a=3时,求函数f(x)的定义域;
(2)若g(x)=f(x)﹣loga(3+ax),请判定g(x)的奇偶性;
(3)是否存在实数a,使函数f(x)在[2,3]递增,并且最大值为1,若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x+k,且log2f(a)=2,f(log2a)=k,a>0,且a≠1.
(1)求a,k的值;
(2)当x为何值时,f(logax)有最小值?求出该最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阅读下列材料,回答后面问题:
在2014年12月30日![]() 播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班
播出的“新闻直播间”节目中,主持人说:“……加入此次亚航失联航班![]() 被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
被证实失事的话,2014年航空事故死亡人数将达到1320人.尽管如此,航空安全专家还是提醒:飞机仍是相对安全的交通工具.①世界卫生组织去年公布的数据显示,每年大约有124万人死于车祸,而即使在航空事故死亡人数最多的一年,也就是1972年,其死亡数字也仅为3346人;②截至2014年9月,每百万架次中有2.1次(指飞机失事),乘坐汽车的百万人中其死亡人数在100人左右.”
对上述航空专家给出的①、②两段表述(划线部分),你认为不能够支持“飞机仍是相对安全的交通工具”的所有表述序号为__________,你的理由是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题,其中正确的个数有( )
①由独立性检验可知,有![]() 的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
的把握认为物理成绩与数学成绩有关,某人数学成绩优秀,则他有99%的可能物理优秀.
②两个随机变量相关性越强,则相关系数的绝对值越接近于1;
③在线性回归方程![]() 中,当解释变量
中,当解释变量![]() 每增加一个单位时,预报变量
每增加一个单位时,预报变量![]() 平均增加0.2个单位;
平均增加0.2个单位;
④对分类变量![]() 与
与![]() ,它们的随机变量
,它们的随机变量![]() 的观测值
的观测值![]() 来说,
来说, ![]() 越小,“
越小,“![]() 与
与![]() 有关系”的把握程度越大.
有关系”的把握程度越大.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2 ![]() . (Ⅰ)判断f(x)奇偶性并证明;
. (Ⅰ)判断f(x)奇偶性并证明;
(Ⅱ)用单调性定义证明函数g(x)= ![]() 在函数f(x)定义域内单调递增,并判断f(x)=log2
在函数f(x)定义域内单调递增,并判断f(x)=log2 ![]() 在定义域内的单调性.
在定义域内的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若集合A={x|kx2﹣2x﹣1=0}只有一个元素,则实数k的取值集合为( )
A.{﹣1}
B.{0}
C.{﹣1,0}
D.(﹣∞,﹣1]∪{0}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com