
【题目】在平面直角坐标系中,O为坐标原点,已知向量 ![]() =(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.
=(﹣1,2),又点A(8,0),B(n,t),C(ksinθ,t),θ∈R.
(1)若 ![]() ⊥
⊥ ![]() ,且
,且 ![]() ,求向量
,求向量 ![]() ;
;
(2)若向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,求f(θ)=tsinθ的值域.
共线,常数k>0,求f(θ)=tsinθ的值域.
【答案】
(1)解: ![]() =(n﹣8,t),∵
=(n﹣8,t),∵ ![]() ⊥
⊥ ![]() ,且
,且 ![]() ,∴﹣(n﹣8)+2t=0,
,∴﹣(n﹣8)+2t=0, ![]() =8
=8 ![]() ,
,
解得t=±8,t=8时,n=24;t=﹣8时,n=﹣8.
∴向量 ![]() =(24,8),(﹣8,﹣8).(2)
=(24,8),(﹣8,﹣8).(2) ![]() =(ksinθ﹣8,t),
=(ksinθ﹣8,t),
(2)解:∵向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,∴t=﹣2ksinθ+16,
共线,常数k>0,∴t=﹣2ksinθ+16,
∴f(θ)=tsinθ=﹣2ksin2θ+16sinθ=﹣2k ![]() +
+ ![]() .
.
①k>4时, ![]() ,∴sinθ=
,∴sinθ= ![]() 时,f(θ)=tsinθ取得最大值
时,f(θ)=tsinθ取得最大值 ![]() ,
,
sinθ=﹣1时,f(θ)=tsinθ取得最小值﹣2k﹣16,此时函数f(θ)的值域为 ![]() .
.
②4>k>0时, ![]() >1.∴sinθ=1时,f(θ)=tsinθ取得最大值﹣2k+16,
>1.∴sinθ=1时,f(θ)=tsinθ取得最大值﹣2k+16,
sinθ=﹣1时,f(θ)=tsinθ取得最小值﹣2k﹣16,
此时函数f(θ)的值域为[﹣2k﹣16,﹣2k+16].
【解析】(1) ![]() =(n﹣8,t),由
=(n﹣8,t),由 ![]() ⊥
⊥ ![]() ,且
,且 ![]() ,可得﹣(n﹣8)+2t=0,
,可得﹣(n﹣8)+2t=0, ![]() =8
=8 ![]() ,联立解出即可得出.(2)
,联立解出即可得出.(2) ![]() =(ksinθ﹣8,t),由向量
=(ksinθ﹣8,t),由向量 ![]() 与向量
与向量 ![]() 共线,常数k>0,可得t=﹣2ksinθ+16,f(θ)=tsinθ=﹣2ksin2θ+16sinθ=﹣2k
共线,常数k>0,可得t=﹣2ksinθ+16,f(θ)=tsinθ=﹣2ksin2θ+16sinθ=﹣2k ![]() +
+ ![]() .对k分类讨论,利用三角函数的值域、二次函数的单调性即可得出.
.对k分类讨论,利用三角函数的值域、二次函数的单调性即可得出.
【考点精析】认真审题,首先需要了解平面向量的坐标运算(坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.
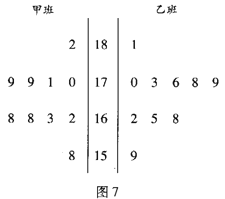
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象的纵坐标不变,横坐标缩短为原来的
的图象的纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象.已知函数
的图象.已知函数![]() .
.
(1)若函数![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)设函数![]() ,证明:对任意
,证明:对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场销售某种品牌的空调器,每周周初购进一定数量的空调器,商场每销售一台空调器可获利500元,若供大于求,则每台多余的空调器需交保管费100元;若供不应求,则可从其他商店调剂供应,此时每台空调器仅获利润200元. (Ⅰ)若该商场周初购进20台空调器,求当周的利润(单位:元)关于当周需求量n(单位:台,n∈N)的函数解析式f(n);
(Ⅱ)该商场记录了去年夏天(共10周)空调器需求量n(单位:台),整理得表:
周需求量n | 18 | 19 | 20 | 21 | 22 |
频数 | 1 | 2 | 3 | 3 | 1 |
以10周记录的各需求量的频率作为各需求量发生的概率,若商场周初购进20台空调器,X表示当周的利润(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中.
(1)设 ![]()
![]() =
= ![]()
![]() ,求证:△ABC是等腰三角形;
,求证:△ABC是等腰三角形;
(2)设向量 ![]() =(2sinC,﹣
=(2sinC,﹣ ![]() ),
), ![]() =(sin2C,2cos2
=(sin2C,2cos2 ![]() ﹣1),且
﹣1),且 ![]() ∥
∥ ![]() ,若sinA=
,若sinA= ![]() ,求sin(
,求sin( ![]() ﹣B)的值.
﹣B)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于R上可导的任意函数f(x),若满足(x﹣2)f′(x)>0,则必有( )
A.f(2)<f(0)<f(﹣3)
B.f(﹣3)<f(0)<f(2)
C.f(0)<f(2)<f(﹣3)
D.f(2)<f(﹣3)<f(0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com