
【题目】设等比数列{an}的公比为q,其前n项之积为Tn,并且满足条件:a1>1,a2 016a2 017>1, ![]() .给出下列结论:(1)0<q<1;(2)a2 016a2 018-1>0;(3)T2 016是数列{Tn}中的最大项;(4)使Tn>1成立的最大正整数n为4 031.其中正确的结论为( )
.给出下列结论:(1)0<q<1;(2)a2 016a2 018-1>0;(3)T2 016是数列{Tn}中的最大项;(4)使Tn>1成立的最大正整数n为4 031.其中正确的结论为( )
A. (2)(3) B. (1)(3)
C. (1)(4) D. (2)(4)
科目:高中数学 来源: 题型:
【题目】共享单车给市民出行带来了诸多便利,某公司购买了一批单车投放到某地给市民使用,
据市场分析,每辆单车的营运累计利润y(单位:元)与营运天数x![]() 满足函数关系
满足函数关系
式![]() .
.
(1)要使营运累计利润高于800元,求营运天数的取值范围;
(2)每辆单车营运多少天时,才能使每天的平均营运利润![]() 的值最大?
的值最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]() 焦点在
焦点在![]() 轴上,且椭圆
轴上,且椭圆![]() 个顶点构成的四边形面积为
个顶点构成的四边形面积为![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆上一点,且
为椭圆上一点,且![]() (
(![]() 为坐标原点).求当
为坐标原点).求当![]() 时,实数
时,实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城镇社区为了丰富辖区内广大居民的业余文化生活,创建了社区“文化丹青”大型活动场所,配备了各种文化娱乐活动所需要的设施,让广大居民健康生活、积极向上.社区最近四年内在“文化丹青”上的投资金额统计数据如表:(为了便于计算,把2015年简记为5,其余以此类推)
年份 | 5 | 6 | 7 | 8 |
投资金额 | 15 | 17 | 21 | 27 |
(1)利用所给数据,求出投资金额![]() 与年份
与年份![]() 之间的回归直线方程
之间的回归直线方程![]() ;
;
(2)预测该社区在2019年在“文化丹青”上的投资金额.
(附:对于一组数据![]() ,
, ![]() ,…,
,…, ![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.互相垂直的两条直线的直观图仍然是互相垂直的两条直线
B.梯形的直观图可能是平行四边形
C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示(把频率当作概率).
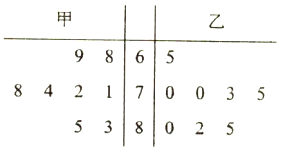
(1)求甲、乙两人成绩的平均数和中位数;
(2)现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E,F,G分别在棱SA,SB,SC上,且平面EFG∥平面ABC,点E为SA的中点.求证:
(Ⅰ)AF⊥平面SBC;
(Ⅱ)SA⊥BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com