
【题目】已知函数![]() (常数
(常数![]() ).
).
(1)讨论![]() 的单调性;
的单调性;
(2)设![]() 是
是![]() 的导函数,求证:
的导函数,求证:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)先求导数,再求导函数零点,根据两零点大小分类讨论,确定导函数符号变化规律,进而确定单调性,(2)先化简所证不等式,再利用导函数证![]() (
(![]() ),即得
),即得![]() (
(![]() ),最后再利用导数证
),最后再利用导数证![]() (差函数或商函数),根据
(差函数或商函数),根据
等号不同时成立得结论.
试题解析:(1)![]() (
(![]() ,
,![]() )
)
画出![]() (
(![]() )及
)及![]() (
(![]() )的图象,它们的零点分别为
)的图象,它们的零点分别为![]() 和
和![]()
①当![]() 时,
时,![]() 在
在![]()
![]() ,
,![]() ,
,![]()
②当![]() 时,
时,![]() 在
在![]()
③当![]() 时,
时,![]() 在
在![]() ,
,![]() ,
,![]()
(2)因![]()
要证![]() ,需证
,需证![]() (
(![]() )
)
法1.即证![]() (
(![]() )
)
设![]() (
(![]() ),
),![]() (
(![]() )
)
一方面![]() (
(![]() )
)![]() 在
在![]() ,
,![]()
则![]() ①
①
另一方面,![]() (
(![]() )
)![]() 在
在![]() ,
,![]()
则![]() ②
②
据①②![]()
有因①的取等条件是![]() ,②的取等条件是
,②的取等条件是![]()
故![]() ,即
,即![]() (
(![]() ),即
),即![]()
法2先证![]() (
(![]() )(差函数)
)(差函数)
进而![]() (
(![]() )
)
再证![]() (差函数或商函数)
(差函数或商函数)
说明等号不成立
故![]() (
(![]() )成立.
)成立.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中数学 来源: 题型:
【题目】一只红铃虫的产卵数y和温度x有关,现收集了6组观测数据于下表中,通过散点图可以看出样本点分布在一条指数型函数y=![]() 的图象的周围.
的图象的周围.
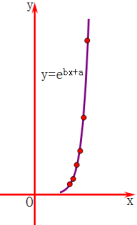
(1)试求出y关于x的上述指数型的回归曲线方程(结果保留两位小数);
(2)试用(1)中的回归曲线方程求相应于点(24,17)的残差![]() .(结果保留两位小数)
.(结果保留两位小数)
温度x(°C) | 20 | 22 | 24 | 26 | 28 | 30 |
产卵数y(个) | 6 | 9 | 17 | 25 | 44 | 88 |
z=lny | 1.79 | 2.20 | 2.83 | 3.22 | 3.78 | 4.48 |
几点说明:
①结果中的![]() 都应按题目要求保留两位小数.但在求
都应按题目要求保留两位小数.但在求![]() 时请将
时请将![]() 的值多保留一位即用保留三位小数的结果代入.
的值多保留一位即用保留三位小数的结果代入.
②计算过程中可能会用到下面的公式:回归直线方程的斜率![]() =
= =
= ,截距
,截距![]() .
.
③下面的参考数据可以直接引用:![]() =25,
=25,![]() =31.5,
=31.5,![]() ≈3.05,
≈3.05,![]() =5248,
=5248,![]() ≈476.08,
≈476.08,![]() ,ln18.17≈2.90.
,ln18.17≈2.90.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某兴趣小组进行“野岛生存”实践活动,他们设置了![]() 个取水敞口箱.其中
个取水敞口箱.其中![]() 个采用
个采用![]() 种取水法,
种取水法,![]() 个采用
个采用![]() 种取水法.如图甲为
种取水法.如图甲为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图,图乙为
个水箱积取淡水量频率分布直方图,图乙为![]() 种方法一个夜晚操作一次
种方法一个夜晚操作一次![]() 个水箱积取淡水量频率分布直方图.
个水箱积取淡水量频率分布直方图.
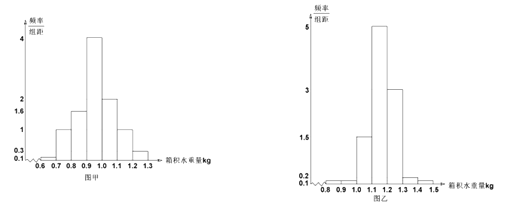
(1)设两种取水方法互不影响,设![]() 表示事件“
表示事件“![]() 法取水箱水量不低于
法取水箱水量不低于![]() ,
,![]() 法取水箱水量不低于
法取水箱水量不低于![]() ”,以样本估计总体,以频率分布直方图中的频率为概率,估计
”,以样本估计总体,以频率分布直方图中的频率为概率,估计![]() 的概率;
的概率;
(2)填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为箱积水量与取水方法有关.
的把握认为箱积水量与取水方法有关.
箱积水量 | 箱积水量 | 箱数总计 | |
| |||
| |||
箱数总计 |
附:![]()
![]()

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为净化新安江水域的水质,市环保局于2017年底在新安江水域投入一些蒲草,这些蒲草在水中的蔓延速度越来越快,2018年二月底测得蒲草覆盖面积为![]() ,2018年三月底测得覆盖面积为
,2018年三月底测得覆盖面积为![]() ,蒲草覆盖面积
,蒲草覆盖面积![]() (单位:
(单位:![]() )与月份
)与月份![]() (单位:月)的关系有两个函数模型
(单位:月)的关系有两个函数模型![]() 与
与![]() 可供选择.
可供选择.
(Ⅰ)分别求出两个函数模型的解析式;
(Ⅱ)若市环保局在2017年年底投放了![]() 的蒲草,试判断哪个函数模型更合适?并说明理由;
的蒲草,试判断哪个函数模型更合适?并说明理由;
(Ⅲ)利用(Ⅱ)的结论,求蒲草覆盖面积达到![]() 的最小月份.
的最小月份.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为2的正方形ABCD中,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使得平面A′DE⊥平面BCDE,F为线段A′C的中点.
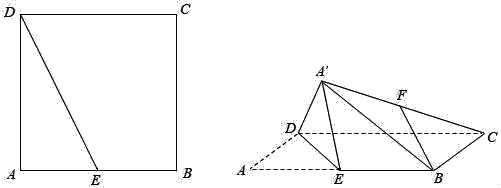
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)求直线A′B与平面A′DE所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 各条棱的长度均相等,
各条棱的长度均相等,![]() 为
为![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 上的动点(含端点),且满足
上的动点(含端点),且满足![]() ,当
,当![]() 运动时,下列结论中不正确的是( )
运动时,下列结论中不正确的是( )

A. 在![]() 内总存在与平面
内总存在与平面![]() 平行的线段
平行的线段
B. 平面![]() 平面
平面![]()
C. 三棱锥![]() 的体积为定值
的体积为定值
D. ![]() 可能为直角三角形
可能为直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,下列说法错误的是( )
,下列说法错误的是( )
A. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
B. 若![]() 有最大值,则
有最大值,则![]() 也有最大值
也有最大值
C. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
D. 若数列![]() 不单调,则数列
不单调,则数列![]() 也不单调
也不单调
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:


(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数分布直方图;
(3)若成绩在75.585.5分的学生为二等奖,问获得二等奖的学生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com