
【题目】如图,在四棱柱ABCD-A1B1C1D1中,AB![]() CD,AB1⊥BC,且AA1=AB.求证:
CD,AB1⊥BC,且AA1=AB.求证:
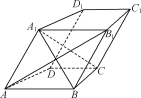
(1)AB![]() 平面D1DCC1;
平面D1DCC1;
(2)AB1⊥平面A1BC.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1) 在四棱柱中得出AB∥CD,结合线面平行的判定定理,即可证得AB![]() 平面D1DCC1;
平面D1DCC1;
(2) 先证得AB1⊥A1B,AB1⊥BC,结合线面垂直的判定定理,即可得到AB1⊥平面A1BC.
(1) 在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB![]() 平面D1DCC1,CD
平面D1DCC1,CD![]() 平面D1DCC1,
平面D1DCC1,
所以AB∥平面D1DCC1.
(2) 在四棱柱ABCD-A1B1C1D1中,四边形A1ABB1为平行四边形,
又AA1=AB,故四边形A1ABB1为菱形,
从而AB1⊥A1B,
又AB1⊥BC,而A1B∩BC=B,A1B、BC![]() 平面A1BC,
平面A1BC,
所以AB1⊥平面A1BC.


科目:高中数学 来源: 题型:
【题目】已知直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)若![]() ,求曲线
,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】足球运动被誉为“世界第一运动”.为推广足球运动,某学校成立了足球社团由于报名人数较多,需对报名者进行“点球测试”来决定是否录取,规则如下:
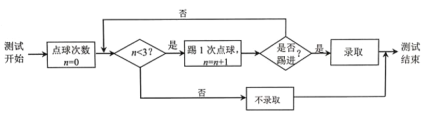
(1)下表是某同学6次的训练数据,以这150个点球中的进球频率代表其单次点球踢进的概率.为加入足球社团,该同学进行了“点球测试”,每次点球是否踢进相互独立,将他在测试中所踢的点球次数记为![]() ,求
,求![]() ;
;
![]()
(2)社团中的甲、乙、丙三名成员将进行传球训练,从甲开始随机地将球传给其他两人中的任意一人,接球者再随机地将球传给其他两人中的任意一人,如此不停地传下去,且假定每次传球都能被接到.记开始传球的人为第1次触球者,接到第n次传球的人即为第![]() 次触球者
次触球者![]() ,第n次触球者是甲的概率记为
,第n次触球者是甲的概率记为![]() .
.
(i)求![]() ,
,![]() ,
,![]() (直接写出结果即可);
(直接写出结果即可);
(ii)证明:数列![]() 为等比数列.
为等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂的某种产品成箱包装,每箱20件,每一箱产品在交付用户时,用户要对该箱中部分产品作检验.设每件产品为不合格品的概率都为![]() ,且各件产品是否合格相互独立.
,且各件产品是否合格相互独立.
(1)记某一箱20件产品中恰有2件不合格品的概率为![]() ,
,![]() 取最大值时对应的产品为不合格品概率为
取最大值时对应的产品为不合格品概率为![]() ,求
,求![]() ;
;
(2)现从某一箱产品中抽取3件产品进行检验,以(1)中确定的![]() 作为p的值,已知每件产品的检验费用为10元,若检验出不合格品,则工厂要对每件不合格品支付30元的赔偿费用,检验费用与赔偿费用的和记为
作为p的值,已知每件产品的检验费用为10元,若检验出不合格品,则工厂要对每件不合格品支付30元的赔偿费用,检验费用与赔偿费用的和记为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 将
将![]() 的图象上所有点向左平移
的图象上所有点向左平移![]() 个单位,然后纵坐标不变,横坐标缩短为原来的
个单位,然后纵坐标不变,横坐标缩短为原来的![]() ,得到函数
,得到函数![]() 的图象.若
的图象.若![]() 为偶函数,且最小正周期为
为偶函数,且最小正周期为![]() ,则( )
,则( )
A.![]() 图象与
图象与![]() 对称B.
对称B.![]() 在
在![]() 单调递增
单调递增
C.![]() 在
在![]() 有且仅有3个解D.
有且仅有3个解D.![]() 在
在![]() 有仅有3个极大值点
有仅有3个极大值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,平面CDEF⊥平面ABCD,且四边形ABCD为平行四边形,∠DAB=45°,四边形CDEF为直角梯形,EF∥DC,ED⊥CD,AB=3EF=3,ED=a,AD![]() .
.
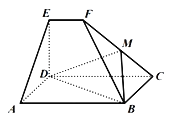
(1)求证:AD⊥BF;
(2)若线段CF上存在一点M,满足AE∥平面BDM,求![]() 的值;
的值;
(3)若a=1,求二面角D﹣BC﹣F的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.已知直线
轴正半轴为极轴建立极坐标系.已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过动点![]() 且平行于
且平行于![]() 的直线交曲线
的直线交曲线![]() 于
于![]() 两点,若
两点,若![]() ,求动点
,求动点![]() 到直线
到直线![]() 的最近距离.
的最近距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com