
【题目】为迎接2017年“双![]() ”,“双
”,“双![]() ”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共
”购物狂欢节的来临,某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共![]() 个,生产一个汤碗需
个,生产一个汤碗需![]() 分钟,生产一个花瓶需
分钟,生产一个花瓶需![]() 分钟,生产一个茶杯需
分钟,生产一个茶杯需![]() 分钟,已知总生产时间不超过
分钟,已知总生产时间不超过![]() 小时.若生产一个汤碗可获利润
小时.若生产一个汤碗可获利润![]() 元,生产一个花瓶可获利润
元,生产一个花瓶可获利润![]() 元,生产一个茶杯可获利润
元,生产一个茶杯可获利润![]() 元.
元.
(1)使用每天生产的汤碗个数![]() 与花瓶个数
与花瓶个数![]() 表示每天的利润
表示每天的利润![]() (元);
(元);
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
【答案】(1)![]() ;(2)
;(2)![]() 元.
元.
【解析】试题分析:(1)由题意可得利润ω=5x+6y+3(100-x-y)=2x+3y+300;(2)根据题意得到约束条件和目标函数,根据线性规划的解题步骤求解即可。
试题解析:
(1)依题意每天生产的茶杯个数为100-x-y,
所以利润ω=5x+6y+3(100-x-y)=2x+3y+300.
(2)由条件得约束条件为
 ,即
,即 ,
,
目标函数为ω=2x+3y+300,
作出不等式组表示的平面区域(如图所示),

作初始直线l0:2x+3y=0,平移l0,由图形知当l0经过点A时,直线在y轴上的截距最大,此时ω有最大值,
由![]() ,解得
,解得![]()
∴最优解为A(50,50),
∴![]() 元.
元.
故每天生产汤碗50个,花瓶50个,茶杯0个时利润最大,且最大利润为550元.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:高中数学 来源: 题型:
【题目】河南多地遭遇跨年霾,很多学校调整元旦放假时间,提前放假让学生们在家里躲霾,郑州市根据《郑州市人民政府办公厅关于将重污染天气黄色预警升级为红色预警的通知》.自12月29日12时将黄色预警升级为红色预警,12月30日0时启动I级响应,明确要求:“幼儿园、中小学等教育机构停课,停课不停学”,学生和家长对停课这一举措褒贬不一,有为了健康赞成的,有怕耽误学习不赞成的.某调查机构为了了解公众对该举措的态度,随机调查采访了50人,将调查情况整理汇总成下表:
年龄(岁) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)请补全被调查人员年龄的频率分布直方图;

(2)若从年龄在![]() 的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
的被调查者中分别随机选取一人进行追踪调查,求这两人都赞成“停课”这一举措的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() (
(![]() 为参数,
为参数, ![]() ),其中
),其中![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() ,曲线
,曲线![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的直角坐标系;
交点的直角坐标系;
(Ⅱ)若![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某蔬菜商店买进的土豆![]() (吨)与出售天数
(吨)与出售天数![]() (天)之间的关系如表所示:
(天)之间的关系如表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |

(Ⅰ)请根据表中数据在所给网格中绘制散点图;
(Ⅱ)请根据表中提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (其中
(其中![]() 保留2位有效数字);
保留2位有效数字);
(Ⅲ)根据(Ⅱ)中的计算结果,若该蔬菜商店买进土豆40吨,则预计可以销售多少天(计算结果保留整数)?
附: 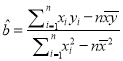 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 的直线
的直线![]() 与中心在原点,焦点在
与中心在原点,焦点在![]() 轴上且离心率为
轴上且离心率为![]() 的椭圆
的椭圆![]() 相交于
相交于![]() 、
、![]() 两点,直线
两点,直线![]() 过线段
过线段![]() 的中点,同时椭圆
的中点,同时椭圆![]() 上存在一点与右焦点关于直线
上存在一点与右焦点关于直线![]() 对称.
对称.
(1)求直线![]() 的方程;
的方程;
(2)求椭圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义函数y=f(x),x∈D(定义域),若存在常数C,对于任意x1∈D,存在唯一的x2∈D,使得 ![]() =C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
=C,则称函数f(x)在D上的“均值”为C,已知f(x)=lgx,x∈[10,100],则函数f(x)在[10,100]上的均值为( )
A.![]()
B.![]()
C.![]()
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“足寒伤心,民寒伤国”,精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对石山区乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本
(其中推广促销费不能超过3万元).已知加工此批农产品还要投入成本![]() 万元(不包含推广促销费用),若加工后的每件成品的销售价格定为
万元(不包含推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润
万元的函数;(利润![]() 销售额
销售额![]() 成本
成本![]() 推广促销费)
推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定下列函数:①f(x)= ![]() ②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
②f(x)=﹣|x|③f(x)=﹣2x﹣1 ④f(x)=(x﹣1)2 , 满足“对任意x1 , x2∈(0,+∞),当x1<x2时,都有f(x1)>f(x2)”的条件是( )
A.①②③
B.②③④
C.①②④
D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com