
(2005
福建,21)如下图,已知方向向量为 的直线l过点(0,
的直线l过点(0, )和椭圆C:
)和椭圆C: (a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(a>b>0)的焦点,且椭圆C的中心关于直线l的对称点在椭圆C的右准线上.
(1)
求椭圆C的方程;(2)
是否存在过点E(-2,0)的直线m交椭圆C于点M、N,满足 .若存在,求直线m的方程;若不存在,请说明理由.
.若存在,求直线m的方程;若不存在,请说明理由.

|
解析:解法一: (1)直线 . ① . ①
过原点垂直 l的直线方程为 . ② . ②
解①②得 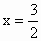 . .
∵椭圆中心 O(0,0)关于直线l的对称点在椭圆C的右准线上,∴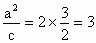 . .
∵直线 l过椭圆焦点,∴该焦点坐标为(2,0).∴ c=2,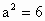 , ,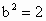 . .
故椭圆 C的方程为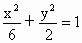 . ③ . ③
解法二:直线 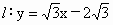 . .
设原点关于直线 l的对称点为(p,q),则
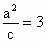 . .
∵直线 l过椭圆焦点,∴该焦点坐标为(2,0).∴ c=2,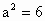 , ,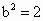 .故椭圆C的方程为 .故椭圆C的方程为 . ③ . ③
(2) 解法一:设M( , ,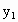 )、N( )、N(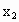 , , ). ).
如下图,当直线 m不垂直x轴时,直线m∶y=k(x+2)代入③,整理得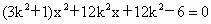 , ,
∴ 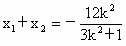 , ,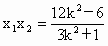 , ,
点 O到直线MN的距离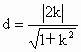 . .
∵ 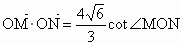 , ,
即 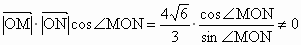 , ,
∴ 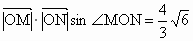 . .
∴ 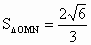 .∴ .∴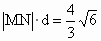 , ,
即 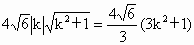 ,整理得 ,整理得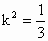 .故 .故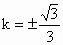 , ,
如下图,当直线 m垂直x轴时,也满足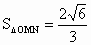 . .
故直线 m的方程为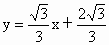
或 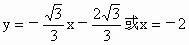 . .
经检验上述直线均满足 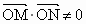 . .
所以所求直线方程为 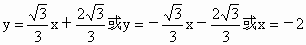 . .
解法二:设 M( , ,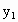 )、N( )、N(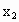 , , ). ).
当直线 m不垂直x轴时,直线m∶y=k(x+2)代入③,整理得 ,于是 ,于是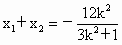 . .
∵ E(-2,0)是椭圆C的左焦点,∴ 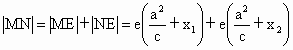
以下与解法一相同. |
|
剖析:本题考查向量、椭圆及对称等综合知识,考查直线与椭圆的位置关系. |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com