
°æƒø°ø‘⁄—ßœ∞∫Ø ˝ ±£¨Œ“√«æ≠¿˙¡À°∞»∑∂®∫Ø ˝µƒ±Ì¥Ô Ω¿˚”√∫Ø ˝ÕºœÛ—–æø∆‰–‘÷ °™°™‘À”√∫Ø ˝Ω‚戌 °∞µƒ—ßœ∞π˝≥㨑⁄ª≠∫Ø ˝ÕºœÛ ±£¨Œ“√«Õ®π˝¡–±Ì°¢√˵„°¢¡¨œþµƒ∑Ω∑®ª≠≥ˆ¡ÀÀ˘—ßµƒ∫Ø ˝ÕºœÛ£ÆÕ¨ ±£¨Œ“√«“≤—ßœ∞π˝æ¯∂‘÷µµƒ“‚“Â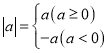 £Æ
£Æ
Ω·∫œ…œ√Êæ≠¿˙µƒ—ßœ∞π˝≥㨜÷‘⁄¿¥Ω‚戜¬√ʵƒŒ £∫
‘⁄∫Ø ˝![]() ÷–£¨µ±
÷–£¨µ±![]() ±£¨
±£¨![]() £ªµ±
£ªµ±![]() ±£¨
±£¨![]() £Æ
£Æ
£®1£©«Û’‚∏ˆ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©‘⁄∏¯≥ˆµƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨«Î÷±Ω”ª≠≥ˆ¥À∫Ø ˝µƒÕºœÛ≤¢–¥≥ˆ’‚∏ˆ∫Ø ˝µƒ¡ΩÃı–‘÷ £ª
£®3£©‘⁄Õº÷–◊˜≥ˆ∫Ø ˝![]() µƒÕºœÛ£¨Ω·∫œƒ„À˘ª≠µƒ∫Ø ˝ÕºœÛ£¨÷±Ω”–¥≥ˆ≤ªµ» Ω
µƒÕºœÛ£¨Ω·∫œƒ„À˘ª≠µƒ∫Ø ˝ÕºœÛ£¨÷±Ω”–¥≥ˆ≤ªµ» Ω![]() µƒΩ‚ºØ£Æ
µƒΩ‚ºØ£Æ
°æ¥∞∏°ø£®1£©![]() £ª£®2£©ÕºœÛ°¢–‘÷ º˚Ω‚Œˆ£ª£®3£©
£ª£®2£©ÕºœÛ°¢–‘÷ º˚Ω‚Œˆ£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©Ω´µ„![]() °¢
°¢![]() µƒ◊¯±Í¥˙»Î∫Ø ˝
µƒ◊¯±Í¥˙»Î∫Ø ˝![]() µƒΩ‚Œˆ Ω£¨«Û≥ˆ
µƒΩ‚Œˆ Ω£¨«Û≥ˆ![]() ∫Õ
∫Õ![]() µƒ÷µ£¨”…¥Àø…µ√≥ˆ∏√∫Ø ˝µƒΩ‚Œˆ Ω£ª
µƒ÷µ£¨”…¥Àø…µ√≥ˆ∏√∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©”…“‚∏˘æð£®1£©÷–µƒ±Ì¥Ô Ωø…“‘ª≠≥ˆ∏√∫Ø ˝µƒÕºœÛ£¨Ω·∫œÕºœÛø…µ√≥ˆ∏√∫Ø ˝µƒ∂‘≥∆–‘”ε•µ˜–‘£ª
£®3£©”…“‚∏˘æðÕºœÛø…“‘÷±Ω”–¥≥ˆÀ˘«Û≤ªµ» ΩµƒΩ‚ºØ£Æ
£®1£©Ω´µ„![]() °¢
°¢![]() µƒ◊¯±Í¥˙»Î∫Ø ˝
µƒ◊¯±Í¥˙»Î∫Ø ˝![]() µƒΩ‚Œˆ Ω£¨µ√
µƒΩ‚Œˆ Ω£¨µ√ £¨Ω‚µ√
£¨Ω‚µ√![]() ,
,
À˘“‘£¨∫Ø ˝µƒΩ‚Œˆ ΩŒ™![]() £ª
£ª
£®2£©ÕºœÛ»Áœ¬£∫

∫Ø ˝![]() µƒÕºœÛπÿ”⁄÷±œþ
µƒÕºœÛπÿ”⁄÷±œþ![]() ∂‘≥∆£¨∏√∫Ø ˝µƒµ•µ˜µðºı«¯º‰Œ™
∂‘≥∆£¨∏√∫Ø ˝µƒµ•µ˜µðºı«¯º‰Œ™![]() £¨µ•µ˜µð‘ˆ«¯º‰Œ™
£¨µ•µ˜µð‘ˆ«¯º‰Œ™![]() £¨◊Ó–°÷µŒ™
£¨◊Ó–°÷µŒ™![]() £ª
£ª
£®3£©ÕºœÛ»Áœ¬£¨

π€≤ÏÕºœÛø…µ√≤ªµ» Ω![]() µƒΩ‚ºØŒ™£∫
µƒΩ‚ºØŒ™£∫![]() £Æ
£Æ


 √˚ ¶µ„≤¶æÌœµ¡–¥∞∏
√˚ ¶µ„≤¶æÌœµ¡–¥∞∏ ”¢≤≈º∆ªÆ∆⁄ƒ©µ˜—–œµ¡–¥∞∏
”¢≤≈º∆ªÆ∆⁄ƒ©µ˜—–œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥ÃÔæ∂∂””–»˝√˚∂Ã≈БÀ∂Ø‘±£¨∏˘æð∆Ω ±—µ¡∑«ÈøˆÕ≥º∆º◊°¢““°¢±˚»˝»À100√◊≈У®ª•≤ª”∞œÏ£©µƒ≥…º®∫œ∏Òµƒ∏≈¬ ∑÷±Œ™![]() £¨
£¨![]() £¨
£¨![]() £¨»Ù∂‘’‚»˝√˚∂Ã≈БÀ∂Ø‘±µƒ100√◊≈еƒ≥…º®Ω¯––“ª¥ŒºÏ≤‚.
£¨»Ù∂‘’‚»˝√˚∂Ã≈БÀ∂Ø‘±µƒ100√◊≈еƒ≥…º®Ω¯––“ª¥ŒºÏ≤‚.
£®1£©«Û»˝»À∂º∫œ∏Òµƒ∏≈¬ £ª
£®2£©«Û»˝»À∂º≤ª∫œ∏Òµƒ∏≈¬ £ª
£®3£©«Û≥ˆœ÷º∏»À∫œ∏Òµƒ∏≈¬ ◊Ó¥Û.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øŒ™¡À∑¥”≥π˙√Òæ≠º√∏˜––“µ∂‘≤÷¥¢ŒÔ¡˜“µŒÒµƒ–Ë«Û±‰ªØ«Èøˆ£¨“‘º∞÷ÿ“™…Ã∆∑ø‚¥Ê±‰ªØµƒ∂؜ڣ¨÷–π˙ŒÔ¡˜”Î≤…π∫¡™∫œª·∫Õ÷–¥¢∑¢’ππ…∑ð”–œÞπ´ÀæÕ®π˝¡™∫œµ˜≤È£¨÷∆∂®¡À÷–π˙≤÷¥¢÷∏ ˝£Æ»ÁÕºÀ˘ 浃’€œþÕº «2016ƒÍ1‘¬÷¡2017ƒÍ12‘¬µƒ÷–π˙≤÷¥¢÷∏ ˝◊þ ∆«Èøˆ£Æ

∏˘æð∏√’€œþÕº£¨œ¬¡–Ω·¬€’˝»∑µƒ «
A. 2016ƒÍ∏˜‘¬µƒ≤÷¥¢÷∏ ˝◊Ó¥Û÷µ «‘⁄3‘¬∑ð
B. 2017ƒÍ1‘¬÷¡12‘¬µƒ≤÷¥¢÷∏ ˝µƒ÷–Œª ˝Œ™54%
C. 2017ƒÍ1‘¬÷¡4‘¬µƒ≤÷¥¢÷∏ ˝±»2016ƒÍÕ¨∆⁄≤®∂Ø–‘∏¸¥Û
D. 2017ƒÍ11‘¬µƒ≤÷¥¢÷∏ ˝Ωœ…œ‘¬”–À˘ªÿ¬‰£¨œ‘ æ≥ˆ≤÷¥¢“µŒÒªÓ∂Ø»‘»ªΩœŒ™ªÓ‘棨æ≠º√‘À––Œ»÷–œÚ∫√
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Õ÷‘≤![]() µƒ¡Ω∏ˆΩπµ„∑÷±Œ™
µƒ¡Ω∏ˆΩπµ„∑÷±Œ™![]() °¢
°¢![]() £¨
£¨![]() Œ™Õ÷‘≤
Œ™Õ÷‘≤![]() µƒ“ª∏ˆ∂Ã÷·∂•µ„£¨
µƒ“ª∏ˆ∂Ã÷·∂•µ„£¨![]() £Æ
£Æ
£®1£©«ÛÕ÷‘≤![]() µƒ±Í◊º∑Ω≥ãª
µƒ±Í◊º∑Ω≥ãª
£®2£©»Ùæ≠π˝Õ÷‘≤![]() ◊ÛΩ𵄵ƒ÷±œþ
◊ÛΩ𵄵ƒ÷±œþ![]() ΩªÕ÷‘≤
ΩªÕ÷‘≤![]() ”⁄
”⁄![]() °¢
°¢![]() ¡Ωµ„£¨
¡Ωµ„£¨![]() Œ™Õ÷‘≤
Œ™Õ÷‘≤![]() µƒ”“∂•µ„£¨«Û
µƒ”“∂•µ„£¨«Û![]() √ʪ˝µƒ◊Ó¥Û÷µ£Æ
√ʪ˝µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™«ÚO «’˝»˝¿‚◊∂£®µ◊√ÊŒ™’˝»˝Ω«–Œ£¨∂•µ„‘⁄µ◊√ʵƒ…‰”∞Œ™µ◊√Ê÷––ƒ£©A-BCDµƒÕ‚Ω”«Ú£¨BC=3£¨![]() £¨µ„E‘⁄œþ∂ŒBD…œ£¨«“BD=3BE£¨π˝µ„E◊˜‘≤OµƒΩÿ√Ê£¨‘ÚÀ˘µ√Ωÿ√Ê‘≤√ʪ˝µƒ»°÷µ∑∂Œß «__.
£¨µ„E‘⁄œþ∂ŒBD…œ£¨«“BD=3BE£¨π˝µ„E◊˜‘≤OµƒΩÿ√Ê£¨‘ÚÀ˘µ√Ωÿ√Ê‘≤√ʪ˝µƒ»°÷µ∑∂Œß «__.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() µƒÕºœÛæ≠π˝µ„£®
µƒÕºœÛæ≠π˝µ„£®![]() £¨
£¨![]() £©∫Õ£®
£©∫Õ£®![]() £¨
£¨![]() £©£¨ÕÍ≥…œ¬√ÊŒ £∫
£©£¨ÕÍ≥…œ¬√ÊŒ £∫

£®1£©«Û∫Ø ˝![]() µƒ±Ì¥Ô Ω£ª
µƒ±Ì¥Ô Ω£ª
£®2£©‘⁄∏¯≥ˆµƒ∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨«Î”√ µ±µƒ∑Ω∑®ª≠≥ˆ’‚∏ˆ∫Ø ˝µƒÕºœÛ£¨≤¢–¥≥ˆ’‚∏ˆ∫Ø ˝µƒ“ªÃı–‘÷ £ª
£®3£©“—÷™∫Ø ˝![]() µƒÕºœÛ»ÁÕºÀ˘ æ£¨Ω·∫œƒ„À˘ª≠≥ˆ
µƒÕºœÛ»ÁÕºÀ˘ æ£¨Ω·∫œƒ„À˘ª≠≥ˆ![]() µƒÕºœÛ£¨÷±Ω”–¥≥ˆ
µƒÕºœÛ£¨÷±Ω”–¥≥ˆ![]() µƒΩ‚ºØ£Æ
µƒΩ‚ºØ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∞ý°∞ ˝—ß–À»§–°◊È°±∂‘∫Ø ˝y£Ω©Åx2+2|x|+1µƒÕºœÛ∫Õ–‘÷ Ω¯––¡ÀÃΩæø£¨ÃΩæøπ˝≥ûÁœ¬£¨«Î≤π≥‰ÕÍ’˚£Æ
£®1£©◊‘±‰¡øxµƒ»°÷µ∑∂Œß «»´Ã µ ˝£¨x”Îyµƒº∏◊È∂‘”¶÷µ¡–±Ì»Áœ¬£∫
x | °≠ | ©Å3 | ©Å | ©Å2 | ©Å1 | 0 | 1 | 2 |
| 3 | °≠ |
y | °≠ | ©Å2 |
| m | 2 | 1 | 2 | 1 |
| ©Å2 | °≠ |
∆‰÷–£¨m£Ω°°°°£Æ
£®2£©∏˘æð…œ±Ì ˝æ𣨑⁄»ÁÕºÀ˘ 浃∆Ω√Ê÷±Ω«◊¯±Íœµ÷–√˵„£¨ª≠≥ˆ¡À∫Ø ˝ÕºœÛµƒ“ª≤ø∑÷£¨«Îª≠≥ˆ∏√∫Ø ˝ÕºœÛµƒ¡Ì“ª≤ø∑÷£Æ
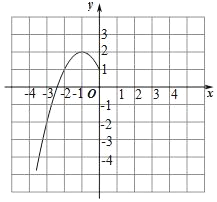
£®3£©π€≤Ï∫Ø ˝ÕºœÛ£¨–¥≥ˆ¡ΩÃı∫Ø ˝µƒ–‘÷ £Æ/p>
£®4£©Ω¯“ª≤ΩÃΩæø∫Ø ˝ÕºœÛ∑¢œ÷£∫
¢Ÿ∑Ω≥éÅx2+2|x|+1£Ω0”–°°°°∏ˆ µ ˝∏˘£ª
¢⁄πÿ”⁄xµƒ∑Ω≥éÅx2+2|x|+1£Ωa”–4∏ˆ µ ˝∏˘ ±£¨aµƒ»°÷µ∑∂Œß «°°°°£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øµ˜≤Ȫ˙ππ∂‘ƒ≥∏þø∆ºº––“µΩ¯––µ˜≤ÈÕ≥º∆£¨µ√µΩ∏√––“µ¥”“µ’þ—ß¿˙∑÷≤º…»–ŒÕº∫Õ¥” ¬∏√––“µ∏⁄Œª∑÷≤ºÃı–ŒÕº£¨»ÁÕºÀ˘ 棨≈–∂œ“‘œ¬»˝÷÷Àµ∑®µƒ’˝ŒÛ£∫¢Ÿ∏√∏þø∆ºº––“µ¥”“µ»À‘±÷–—ß¿˙Œ™≤© øµƒ’º“ª∞Γ‘…œ£ª¢⁄∏√∏þø∆ºº––“µ÷–¥” ¬ºº ı∏⁄Œªµƒ»À ˝≥¨π˝◊Ð ˝µƒ30%£ª¢€∏√∏þø∆ºº––“µ÷–¥” ¬‘À”™∏⁄Œªµƒ»À‘±÷˜“™ «±æø∆…˙.


≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ÷”–“ª∏ˆπÿ”⁄∆Ω√ÊÕº–Œµƒ√¸Ã‚£∫»ÁÕº£¨Õ¨“ª∆Ω√ʃ⁄”–¡Ω∏ˆ±þ≥§∂º «2µƒ’˝∑Ω–Œ£¨∆‰÷–“ª∏ˆµƒƒ≥∂•µ„‘⁄¡Ì“ª∏ˆµƒ÷––ƒ£¨‘Ú’‚¡Ω∏ˆ’˝∑Ω–Œ÷ÿµ˛≤ø∑÷µƒ√ʪ˝∫„Œ™______£Æ
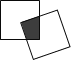
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com