
【题目】某中学高三(2)班甲、乙两名同学自高中以来每次考试成绩的茎叶图如图,下列说法正确的是( )

A.乙同学比甲同学发挥的稳定,且平均成绩也比甲同学高
B.乙同学比甲同学发挥的稳定,但平均成绩不如甲同学高
C.甲同学比乙同学发挥的稳定,且平均成绩也比乙同学高
D.甲同学比乙同学发挥的稳定,但平均成绩不如乙同学高
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)上的点A(4,t)到其焦点F的距离为5.
(Ⅰ)求抛物线C的方程;
(Ⅱ)过点F作直线l,使得抛物线C上恰有三个点到直线1的距离为2,求直线1的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣a)2+(y﹣2)2=4(a>0)及直线l:x﹣y+3=0.当直线l被圆C截得的弦长为![]() 时,求
时,求
(Ⅰ)a的值;
(Ⅱ)求过点(3,5)并与圆C相切的切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,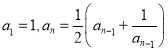 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面是正方形,PD⊥底面ABCD,PD=DC,E是PC的中点.

(1)证明:平面PAB⊥平面PAD;
(2)求二面角P﹣AB﹣D的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P到两点(0,![]() ),(0,
),(0,![]() ),的距离之和等于4,设点P的轨迹为C.
),的距离之和等于4,设点P的轨迹为C.
(1)求C的方程.
(2)设直线![]() 与C交于A,B两点,求弦长|AB|,并判断OA与OB是否垂直,若垂直,请说明理由.
与C交于A,B两点,求弦长|AB|,并判断OA与OB是否垂直,若垂直,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连结DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的二面角BCGA的大小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校所有的1000名学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | 不大于2000元 | 大于2000元 |
仅使用A | 27人 | 3人 |
仅使用B | 24人 | 1人 |
(Ⅰ)估计该校学生中上个月A,B两种支付方式都使用的人数;
(Ⅱ)从样本仅使用B的学生中随机抽取1人,求该学生上个月支付金额大于2000元的概率;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用B的学生中随机抽查1人,发现他本月的支付金额大于2000元.结合(Ⅱ)的结果,能否认为样本仅使用B的学生中本月支付金额大于2000元的人数有变化?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() ,抛物线
,抛物线![]()
![]() 的焦点
的焦点![]() 是
是![]() 的一个顶点,设
的一个顶点,设![]() 是
是![]() 上的动点,且位于第一象限,记
上的动点,且位于第一象限,记![]() 在点
在点![]() 处的切线为
处的切线为![]() .
.

(1)求![]() 的值和切线
的值和切线![]() 的方程(用
的方程(用![]() 表示)
表示)
(2)设![]() 与
与![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与过
与过![]() 且垂直于
且垂直于![]() 轴的直线交于点
轴的直线交于点![]() .
.
(i)求证:点![]() 在定直线上;
在定直线上;
(ii)设![]() 与
与![]() 轴交于点
轴交于点![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com