Question

定义在R上的奇函数f（x）满足：当x＞0时，f（x）=2010^x+log₂₀₁₀x，则在R上方程f（x）=0的实根个数为

1. A.
   1
2. B.
   2
3. C.
   3
4. D.
   4

Answer 1

C
分析：根据f（x）是R上的奇函数，则f（0）=0，当x＞0时，函数f₁（x）=2010^x，f₂（x）=-log₂₀₁₀x的图象有一个交点，知2010^x+log₂₀₁₀x=0有唯一实数根，由奇函数的性质知，当x＜0时，也有唯一一个根使得f（x）=0，从而得到结论．
解答：当x＞0时，令f（x）=0得，即2010^x=-log₂₀₁₀x，
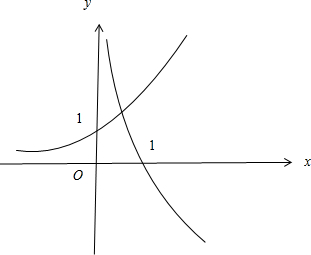
在同一坐标系下分别画出函数f₁（x）=2010^x，f₂（x）=-log₂₀₁₀x的图象，
如右图，可知两个图象只有一个交点，即方程f（x）=0只有一个实根，
∵f（x）是定义在R上的奇函数，
∴当x＜0时，方程f（x）=0也有一个实根，
又∵f（0）=0，
∴方程f（x）=0的实根的个数为3．
故选C．
点评：本题本题主要考查了奇函数图象的性质应用，即根据题意画出一部分函数的图象，由交点的个数求出对应方程根的个数，利用图象的对称性和“f（0）=0”求出方程根的个数，易漏f（0）=0，属于中档题．