
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;

(Ⅱ)试对![]() 与
与![]() 的关系进行相关性检验,如
的关系进行相关性检验,如![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(Ⅲ)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考数据:![]() ,
,![]() .
.
附: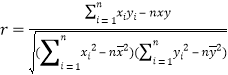 );
); ,
, ![]() ;
;
相关性检验的临界值表
n-2 | 小概率 | n-2 | 小概率 | n-2 | 小概率 | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
注:表中的n为数据的组数
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】商家生产一种产品,需要先进行市场调研,计划对北京、上海、广州三地进行市场调研,待调研结束后决定生产的产品数量,下列四种方案中最可取的是( )
A. ![]()
B. 
C. 
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让观赏游玩更便捷舒适,常州恐龙园推出了代步工具租用服务.已知有脚踏自行车![]() 与电动自行车
与电动自行车![]() 两种车型,采用分段计费的方式租用.
两种车型,采用分段计费的方式租用.![]() 型车每
型车每![]() 分钟收费
分钟收费![]() 元(不足
元(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算),
分钟计算),![]() 型车每
型车每![]() 分钟收费
分钟收费![]() 元(不足
元(不足![]() 分钟的部分按
分钟的部分按![]() 分钟计算),现有甲乙丙丁四人,分别相互独立地到租车点租车骑行(各租一车一次),设甲乙丙丁不超过
分钟计算),现有甲乙丙丁四人,分别相互独立地到租车点租车骑行(各租一车一次),设甲乙丙丁不超过![]() 分钟还车的概率分别为
分钟还车的概率分别为![]() ,并且四个人每人租车都不会超过
,并且四个人每人租车都不会超过![]() 分钟,甲乙丙均租用
分钟,甲乙丙均租用![]() 型车,丁租用
型车,丁租用![]() 型车.
型车.
(1)求甲乙丙丁四人所付的费用之和为25元的概率;
(2)求甲乙丙三人所付的费用之和等于丁所付的费用的概率;
(3)设甲乙丙丁四人所付费用之和为随机变量![]() ,求
,求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
i | 1 | 2 | 3 | 4 | 5 |
|
xi | 2 | 3 | 4 | 5 | 6 | |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | |
xi yi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={a1 , a2 , …,am}.若集合A1∪A2∪A3∪…∪An=A,则称A1 , A2 , A3 , …,An为集合A的一种拆分,所有拆分的个数记为f(n,m).
(1)求f(2,1),f(2,2),f(3,2)的值;
(2)求f(n,2)(n≥2,n∈N*)关于n的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com