
【题目】已知函数f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]() ,x∈R.
,x∈R.
(1)求f(x)的单调递增区间;
(2)在锐角△ABC中,角A,B,C的对边分别a,b,c,若f(A)=![]() ,a=
,a=![]() ,求△ABC面积的最大值.
,求△ABC面积的最大值.
【答案】(1) [kπ﹣![]() ,kπ+
,kπ+![]() ],k∈Z (2)
],k∈Z (2) ![]()
【解析】试题分析:(I)由两角和与差的正弦公式,二倍角的正弦公式与二倍角的余弦公式可将解析式化简为![]() ,由
,由![]() ,可得
,可得![]() 的单调递增区间;(II)由题意可得
的单调递增区间;(II)由题意可得![]() ,结合范围
,结合范围![]() ,解得
,解得![]() 的值,由余弦定理可得结合基本不等式可得
的值,由余弦定理可得结合基本不等式可得![]() ,利用三角形面积公式即可得结果.
,利用三角形面积公式即可得结果.
试题解析:(1)∵f(x)=cosxsin(x+![]() )﹣
)﹣![]() cos2x+
cos2x+![]()
=cosx(![]() sinx+
sinx+![]() cosx)﹣
cosx)﹣![]() cos2x+
cos2x+![]()
=![]() sinxcosx+
sinxcosx+![]() cos2x﹣
cos2x﹣![]() cos2x+
cos2x+![]()
=![]() sin2x﹣
sin2x﹣![]() ×
×![]() +
+![]()
=![]() sin(2x﹣
sin(2x﹣![]() ),
),
由2kπ﹣![]() ≤2x﹣
≤2x﹣![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,解得f(x)的单调递增区间为:[kπ﹣
,k∈Z,解得f(x)的单调递增区间为:[kπ﹣![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
(2)∵f(A)=![]() sin(2A﹣
sin(2A﹣![]() )=
)=![]() ,解得:sin(2A﹣
,解得:sin(2A﹣![]() )=
)=![]() ,
,
∵0![]() ,﹣
,﹣![]() <2A﹣
<2A﹣![]() <
<![]() ,
,
∴解得:2A﹣![]() =
=![]() ,即A=
,即A=![]() .
.
∴由余弦定理可得:3=b2+c2﹣2bccosA=b2+c2﹣bc≥2bc﹣bc=bc,
∴S△ABC=![]() bcsinA=
bcsinA=![]() bc≤
bc≤![]() =
=![]() .
.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
【题目】某学校1800名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,,第五组
,,第五组![]() ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.

(1)若成绩小于15秒认为良好,求该样本在这次百米测试中成绩良好的人数;
(2)请估计学校1800名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知圆O外有一点P,作圆O的切线PM,M为切点,过PM的中点N,作割线NAB,交圆于A,B两点,连接PA并延长,交圆O于点C,连续PB交圆O于点D,若MC=BC. 
(1)求证:△APM∽△ABP;
(2)求证:四边形PMCD是平行四边形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2ln(x+2)﹣(x+1)2 , g(x)=k(x+1).
(1)求f(x)的单调区间;
(2)当k=2时,求证:对于x>﹣1,f(x)<g(x)恒成立;
(3)若存在x0>﹣1,使得当x∈(﹣1,x0)时,恒有f(x)>g(x)成立,试求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为[45,55),[55,65),[65,75),[75,85),[85,95)由此得到频率分布直方图如图.则产品数量位于[55,65)范围内的频率为;这20名工人中一天生产该产品数量在[55,75)的人数是 . 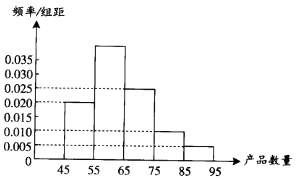
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,等边三角形![]() 的中线
的中线![]() 与中位线
与中位线![]() 相交于
相交于![]() ,已知
,已知![]() 是
是![]() 绕
绕![]() 旋转过程中的一个图形,下列命题中,错误的是
旋转过程中的一个图形,下列命题中,错误的是

A. 恒有![]() ⊥
⊥![]()
B. 异面直线![]() 与
与![]() 不可能垂直
不可能垂直
C. 恒有平面![]() ⊥平面
⊥平面![]()
D. 动点![]() 在平面
在平面![]() 上的射影在线段
上的射影在线段![]() 上
上
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() .
.
(1)若直线![]() 与直线
与直线![]() 平行,求实数
平行,求实数![]() 的值;
的值;
(2)若![]() ,
, ![]() ,点
,点![]() 在直线
在直线![]() 上,已知
上,已知![]() 的中点在
的中点在![]() 轴上,求点
轴上,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据两直线平行,对应方向向量共线,列方程即可求出![]() 的值;(2)根据
的值;(2)根据![]() 时,直线
时,直线![]() 的方程设出点
的方程设出点![]() 的坐标,由此求出
的坐标,由此求出![]() 的中点坐标,再由中点在
的中点坐标,再由中点在![]() 轴上求出点
轴上求出点![]() 的坐标.
的坐标.
试题解析:(1)∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() ,
,
∴![]() ,经检验知,满足题意.
,经检验知,满足题意.
(2)由题意可知: ![]() ,
,
设![]() ,则
,则![]() 的中点为
的中点为![]() ,
,
∵![]() 的中点在
的中点在![]() 轴上,∴
轴上,∴![]() ,
,
∴![]() .
.
【题型】解答题
【结束】
16
【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com