练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    椭圆=1上有n个不同的点P1，P2，…，Pn，椭圆的右焦点为F，数列{|PnF|}是公差大于的等差数列，则n的最大值是(    )

    A．1998                 B．1999              C．2000               D．2001

    答案：C  因数列{|PnF|}的公差d大于，所以它是递增数列，而|P1F|min=1，|PnF|max=3，|PnF|=|P1F|+(n-1)d=d＞n＜1000(|PnF|-|P1F|)+1

    因为(|PnF|-|P1F|)max=3-1=21000(|PnF|-|P1F|)+1的最大值为2001，所以n的最大值为2000．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    椭圆=1上有n个不同的点P1,P2,P3,…,Pn,F是右焦点，|P1F|，|P2F|，…，|PnF|组成公差d＞的等差数列，则n的最大值是(    )

    A.199       B.200        C.99          D.100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    椭圆+=1上有n个不同的点P1、P2、P3、…、Pn,F是右焦点,|P1F|,|P2F|,…,|PnF|组成公差d＞的等差数列,则n的最大值是(    )

    A.199              B.200               C.99               D.100

    查看答案和解析>>

    科目：高中数学 来源：2013届广东省高二上学期期末考试理科数学 题型：选择题

    椭圆+=1上有n个不同的点P1,P2,P3,…,Pn, F是右焦点，|P1F|，|P2F|，…，|PnF|组成等差数列，且公差d>，则n的最大值是（           ）

    A.99                B.100        C.199              D.200  

     

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年广东省揭阳一中高二（上）期末数学试卷（理科）（解析版） 题型：选择题

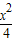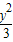    椭圆+=1上有n个不同的点P1，P2，P3，…，Pn，F是右焦点，|P1F|，|P2F|，…，|PnF|组成等差数列，且公差d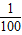＞，则n的最大值是（ ）
    A．99
    B．100
    C．199
    D．200

    查看答案和解析>>

    科目：高中数学 来源：2006年江苏省南京市金陵中学高考数学三模试卷（解析版） 题型：选择题

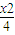    已知椭圆+=1上有n个不同的点P1，P2，P3，…，Pn．设椭圆的右焦点为F，数列{|PnF|}是公差大于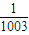的等差数列，则n的最大值为（ ）
    A．2007
    B．2006
    C．1004
    D．1003

    查看答案和解析>>

    同步练习册答案