
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.
C. D.
D.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射击![]() 次,每次中靶环数情况如图所示:
次,每次中靶环数情况如图所示:
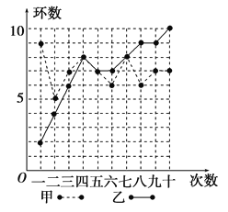
(1)请填写下表(先写出计算过程再填表):
平均数 | 方差 | 命中 | |
甲 |
|
|
|
乙 |
(2)从下列三个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中![]() 环及
环及![]() 环以上的次数相结合看(分析谁的成绩好些);
环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科技创新能力是决定综合国力和国际竞争力的关键因素,也是推动经济实现高质量发展的重要支撑,而研发投入是科技创新的基本保障,下图是某公司从2010年到2019年这10年研发投入的数据分布图:

其中折线图是该公司研发投入占当年总营收的百分比,条形图是当年研发投入的数值(单位:十亿元).
(I)从2010年至2019年中随机选取一年,求该年研发投入占当年总营收的百分比超过10%的概率;
(II)从2010年至2019年中随机选取两个年份,设X表示其中研发投入超过500亿元的年份的个数,求X的分布列和数学期望;
(III)根据图中的信息,结合统计学知识,判断该公司在发展的过程中是否比较重视研发,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a∈R且a≠0).
(a∈R且a≠0).
(1)当a![]() 时,求曲线y=f(x)在点(1,f(1))处的切线方程;
时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)讨论函数f(x)的单调性与单调区间;
(3)若y=f(x)有两个极值点x1,x2,证明:f(x1)+f(x2)<9﹣lna.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为椭圆![]() (a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(a>b>0)的一个焦点,点A为椭圆的右顶点,点B为椭圆的下顶点,椭圆上任意一点到点F距离的最大值为3,最小值为1.
(1)求椭圆的标准方程;
(2)若M、N在椭圆上但不在坐标轴上,且直线AM∥直线BN,直线AN、BM的斜率分别为k1和k2,求证:k1k2=e2﹣1(e为椭圆的离心率).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年春节期间,新型冠状病毒(2019﹣nCoV)疫情牵动每一个中国人的心,危难时刻全国人民众志成城.共克时艰,为疫区助力.我国S省Q市共100家商家及个人为缓解湖北省抗疫消毒物资压力,募捐价值百万的物资对口输送湖北省H市.
(1)现对100家商家抽取5家,其中2家来自A地,3家来自B地,从选中的这5家中,选出3家进行调研.求选出3家中1家来自A地,2家来自B地的概率.
(2)该市一商家考虑增加先进生产技术投入,该商家欲预测先进生产技术投入为49千元的月产增量.现用以往的先进技术投入xi(千元)与月产增量yi(千件)(i=1,2,3,…,8)的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且:
的附近,且:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,
,其中,![]() ,
,![]() ,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
,根据所给的统计量,求y关于x回归方程,并预测先进生产技术投入为49千元时的月产增量.
附:对于一组数据(u1,v1)(u2,v2),其回归直线v=α+βu的斜率和截距的最小二乘法估计分别为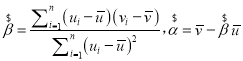
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.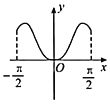
C.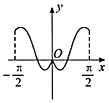 D.
D.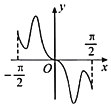
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值点;
的极值点;
(2)定义:若函数![]() 的图像与直线
的图像与直线![]() 有公共点,我们称函数
有公共点,我们称函数![]() 有不动点.这里取:
有不动点.这里取:![]() ,若
,若![]() ,如果函数
,如果函数![]() 存在不动点,求实数
存在不动点,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到其中所有正确结论的编号是( )
个单位得到其中所有正确结论的编号是( )
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com